Maybe the shortest proof that human CO2 does not change the climate.
As part of my reply to Glenn Tamblyn’s comment below, here are Sections 3.3 and 6.1 in Berry (2019).
3.3 Physics Model derivation
A system describes a subset of nature. A system includes levels and flows between levels. Levels set flows and flows set new levels. The mathematics used in the Physics Model are analogous to the mathematics used to describe many engineering systems.
The Physics Model derivation begins with the continuity equation (1) which says the rate of change of level is the difference between inflow and outflow:
dL/dt = Inflow – Outflow (1)
Where
L = CO2 level (concentration in ppm)
t = time (years)
dL/dt = rate of change of L (ppm/year)
Inflow = rate CO2 moves into the system (ppm/year)
Outflow = rate CO2 moves out of the system (ppm/year)
Following the idea from the bucket of water, the Physics Model has only one hypothesis, that outflow is proportional to level:
Outflow = L / Te (2)
where Te is the “turnover time” or “e-time.”
Substitute (2) into (1) to get,
dL/dt = Inflow – L / Te (3)
One way to replace Inflow in (3) is to set dL/dt to zero, which means the level is constant. Then Inflow will equal a balance level, Lb, divided by e-time. However, a more elegant way to replace Inflow is to simply define the balance level, Lb, as
Lb = Inflow * Te (4)
Equation (4) shows how Inflow and Te set the balance level. Substitute (4) for Inflow into (3) to get,
dL/dt = – (L – Lb) / Te (5)
Equation (5) shows the level always moves toward its balance level. At this point, both L and Lb are functions of time. Te can also be a function of time.
In the special case when Lb and Te are constant, there is an analytic solution to (5). Rearrange (5) to get
dL / (L – Lb) = – dt / Te (6)
Then integrate (6) from Lo to L on the left side, and from 0 to t on the right side [29] to get
Ln [(L – Lb) / (Lo – Lb)] = – t / Te (7)
where
Lo = Level at time zero (t = 0)
Lb = the balance level for a given inflow and Te
Te = time for L to move (1 – 1/e) from L to Lb
e = 2.7183
The original integration of (6) contains two absolute values, but they cancel each other because both L and Lo are always either above or below Lb.
Raise e to the power of each side of (7), to get the level as a function of time:
L(t) = Lb + (Lo – Lb) exp(– t/Te) (8)
Equation (8) is the analytic solution of (5) when Lb and Te are constant.
The hypothesis (2) that outflow is proportional to level creates a “balance level.” Equation (4) defines the balance level in terms of inflow and e-time.
Figure 4 shows how the level always moves toward its balance level according to (5). While outflow is always proportional to level, inflow sets the balance level.
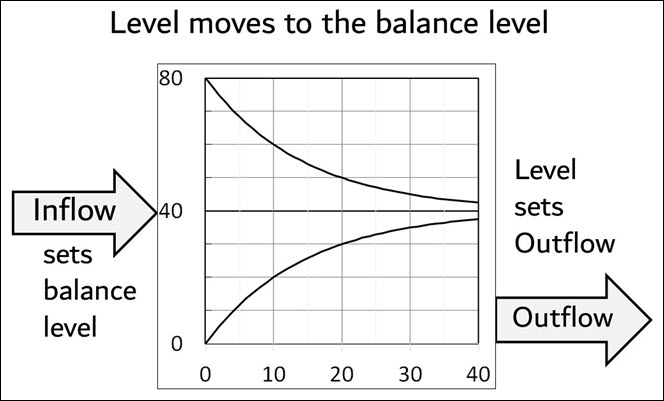
Figure 4. Inflow sets the balance level. The level at any time t determines the outflow. Level always moves toward the balance level, whether the level is above or below the balance level.
The Physics Model shows how CO2 flows through the atmosphere. CO2 does not “stick” in the atmosphere. A higher inflow merely raises the balance level. Then the level will rise until outflow equals inflow, which will be at the balance level.
6.1 IPCC’s response times fail physics
The Physics Model e-time has a precise definition: e-time is the time for the level to move (1 – 1/e) of the distance to its balance level.
Segalstad [10] observes IPCC [3] uses many definitions of lifetime — like residence time, transit time, response time, e-folding time, and adjustment time — in its quest to prove human CO2 remains in the atmosphere for hundreds of years. Many investigators, from 1957 to 1992, have calculated the e-time of atmospheric CO2 is about 5 years [10].
IPCC [3] defines “adjustment time (Ta)” as:
The time-scale characterising the decay of an instantaneous pulse input into the reservoir.
Cawley [5] defines “adjustment time (Ta)” as:
The time taken for the atmospheric CO2 concentration to substantially recover towards its original concentration following a perturbation.
The word “substantially” is imprecise.
Cawley follows IPCC to define “residence time (Tr)” as:
The average length of time a molecule of CO2 remains in the atmosphere before being taken up by the oceans or terrestrial biosphere.
Some authors use “residence time” to mean “e-time” but other authors, such as Cawley and IPCC, have a different meaning for residence time. This paper uses e-time because its definition is precise.
In summary, IPCC uses two different response times when it should use only e-time:
- When the level is far from its balance level (which can be zero), IPCC thinks e-time is an adjustment time because the level is moving rapidly toward its balance level.
- When the level is close to its balance level, IPCC thinks e-time is a residence time because “molecules” are flowing in and out with little change in level.
Figure 14 illustrates how e-time relates to IPCC’s adjustment and residence times.
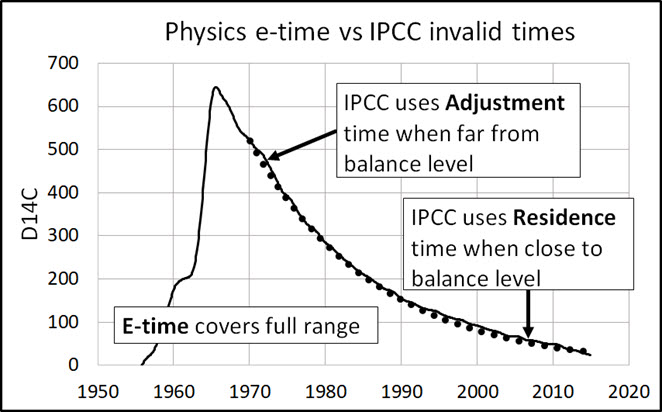
IPCC defines “turnover time (Tt)” as:
The ratio of the mass M of a reservoir (e.g., a gaseous compound in the atmosphere) and the total rate of removal S from the reservoir: Tt = M/S.
IPCC’s turnover time seems to be the same as e-time except “removal” is not the same as outflow. Near the balance level, IPCC sometimes interprets “removal” to mean the difference between outflow and inflow.
IPCC says when outflow is proportional to level (the Physics Model hypothesis) then adjustment time equals turnover time. IPCC claims:
In simple cases, where the global removal of the compound is directly proportional to the total mass of the reservoir, the adjustment time equals the turnover time: Ta = Tt.
The Physics Model’s replication of the 14C data shows the 14CO2 outflow is proportional to level. Therefore, by IPCC’s own definition, adjustment time equals e-time equals residence time.
IPCC says in further confusion:
In more complicated cases, where several reservoirs are involved or where the removal is not proportional to the total mass, the equality T = Ta no longer holds.
Carbon dioxide is an extreme example. Its turnover time is only about 4 years because of the rapid exchange between atmosphere and the ocean and terrestrial biota.
Although an approximate value of 100 years may be given for the adjustment time of CO2 in the atmosphere, the actual adjustment is faster initially and slower later on.
IPCC agrees 12CO2 turnover time (e-time) is about 4 years. IPCC claims adjustment time is “fast initially and slower later on” which is why its Bern model cannot replicate the 14C data in Figure 9.
The 14C data show the e-time for 14CO2 is 16.5 years. This e-time is the upper bound for 12CO2 e-time. The IPCC claim of hundreds of years is based on IPCC’s misunderstanding of e-time.
Unfortunately, there are many different definitions of residence time. Therefore, this paper uses e-time with its exact definition.

I think your ninth slide has a mistake. I think the red dotted line and black line have their labels reversed, as in the text below you seem to say the reverse.
Dear Nigel,
Thank you. You are correct.
Now, I will fix this error.
Ed
The Carbon-14 argument is actually the smoking gun. If the facts given reflect reality, carbon-14-level would necessarily be reduced. The only other explanation would be, that there is an unknown mechanism that bolts carbon-14 to it’s respective level.
Sorry Ed, a deeply flawed analysis,
Lets start with some terminology
From the Glossary of the 4th Assessment Report (AR4)
“Lifetime
Lifetime is a general term used for various time scales
characterizing the rate of processes affecting the concentration of
trace gases. The following lifetimes may be distinguished:
Turnover time (T) (also called global atmospheric lifetime) is the
ratio of the mass M of a reservoir (e.g., a gaseous compound in the
atmosphere) and the total rate of removal S from the reservoir: T = M
/ S. For each removal process, separate turnover times can be defined.
In soil carbon biology, this is referred to as Mean Residence Time.”
So there is the first thing you reference. This is the average time a CO2 molecule, any CO2 molecule,will remain in the atmosphere before it moves into the ocean (or other sink). It is the characteristic flow rate in one direction.
“Adjustment time or response time (Ta ) is the time scale characterising the decay of an instantaneous pulse input into the reservoir. The term adjustment time is also used to characterise the adjustment of the mass of a reservoir following a step change in the source strength. Half-life or decay constant is used to quantify a first-order exponential decay process. See response time for a different definition pertinent to climate variations. The term lifetime is sometimes used, for
simplicity, as a surrogate for adjustment time.”
Why do they define a second time constant?
Because one needs to take account of another flow that you haven’t mentioned. Flows OUT OF the ocean (and other reservoirs) INTO the atmosphere. Your diagram shows flows in only one direction, when the flows are actually bidirectional. Adjustment time is the characteristic response time when allowing for both flows, and also changes in both flows.
Think about this.
If CO2 is added to the atmosphere, then the flow rate of CO2 INTO the oceans will increase. At the same time, this increased flow of CO2 into the ocean is increasing the concentration of carbon in the ocean (just referring to CO2 is chemically inaccurate). This results in the flow rate of CO2 OUT OF the ocean also increasing. Counteracting some of the decline in the atmosphere.
Your diagram is simplistic since it only shows flows in one direction.
Both the ocean and the atmosphere are ‘relaxing’ towards a new balance of concentrations. But this is an exponential decay process so reaching a final new balance takes much longer than the simple Turnover time suggests.
And importantly to note. The increased outflow of CO2 molecules out of the ocean may not be THE SAME molecules that caused the initial increase in inflow.
The IPCC does not say that HUMAN CO2 remains for 1000’s of years – please provide a link to where you actually read this.
Rather human CO2 causes a perturbation in the CO2 balance between atmosphere and ocean and it takes longer for this perturbation to ‘relax’, as CO2 molecules, both natural and man-made, exchange backwards and forwards continuously.
Next
“In simple cases, where the global removal of the compound is directly proportional to the total mass of the reservoir, the adjustment time equals the turnover time: T = Ta. An example is CFC-11, which is removed from the atmosphere only by photochemical processes in the stratosphere. In more complicated cases, where several reservoirs are involved or where the removal is not proportional to the total mass, the equality T = Ta no longer holds. Carbon dioxide (CO 2) is an extreme example. Its turnover time is only about four years because of the rapid exchange between the atmosphere and the ocean and terrestrial biota. However, a large part of that CO2 is returned to the atmosphere within a few years. Thus, the adjustment time of CO2 in the atmosphere is actually determined by the rate of removal of carbon from the surface layer of the oceans into its deeper layers. Although an approximate value of 100 years may be given for the adjustment time of CO2 in the atmosphere, the actual adjustment is faster initially and slower later on. In the case of methane (CH4), the adjustment time is different from the turnover time because the removal is mainly through a chemical reaction with the hydroxyl radical OH, the concentration of which itself depends on the CH 4 concentration. Therefore, the CH4 removal rate S is not proportional to its total mass M.”
Lets look at WHY the IPCC says the adjustment time varies. To do this we need to understand some chemistry and some oceanography.
When CO2 dissolves in water it reacts with water to form Carbonic Acid.
CO2 + H2O H2CO3
Carbonic Acid in turn dissociates into a bicarbonate ion and a hydrogen ion
H2CO3 HCO3- + H+
This in turn dissociates into a carbonate ion and another hydrogen ion.
HCO3- CO3– + H+
I have used reverse arrows because each of these reactions are bidirectional, with rates in both directions.
Most of the Dissolved Inorganic Carbon (DIC) – this isn’t the organic, ‘living things’, aspect – is primarily bicarbonate and carbonate – Carbonic Acid and actual CO2 are a quite small percentage. So the potential rate of exchange of CO2 in the water with CO2 in the atmosphere is coupled to the reaction rate kinematics of the other parts of this chemical chain. Thus not necessarily a simple ‘exchange rate’ question.
Next, Oceanography. The top 50-100 meters of the ocean is called the Mixed (or Well-Mixed) Layer. Wind and wave action mean this is turbulent, and mixes very rapidly. So this is a reservoir where changes in dissolved gases due to exchange at the surface are mixed very rapidly.
The deep ocean is very different.
Vertical mixing due to ocean currents is slow. Typical overturning time for the ocean – how long a drop of water takes to descend from the surface to the abyss, then return to the surface, is of the order of 1000 years. In one sense, when we look at the abyssal ocean we are seeing what the ocean at the surface was like many centuries in the past.
The other method of propagating changes from the surface downward is diffusion. And this is even slower. Multiple lines of evidence show that vertical diffusion in the deep ocean is very, very slow. This is because the deep ocean is profoundly stratified.
If you heat a liquid from the bottom – a pot of water on the stove – or cool it from above, this generates vertical convection, and deep mixing. Conversely, if you heat a liquid from above, this suppresses covective mixing. It becomes highly stratified. And in a stratified liquid, diffusion is slow!
This is the basis for the IPCC’s statements about different, and changing, rates. The ocean isn’t one single reservoir. It is multiple reservoirs, both vertically and by chemical partitioning, with sometimes vastly different rate constants.
Your C14 argument is also completely flawed as well. You don’t seem to understand what the D14C reading actually is. It is not the change in the amount of C14, or the ratio of C14 at different times.
D14C is the delta of the ratio, of the ratio, of C14 to C12 at one time vs the reference C14/C12 ratio – roughly preindustrial.
DC14 is Delta (C14now/C12now) / (C14ref/C12ref)
The bomb pulse from the late 50’s elevated C14 quantities.
Some of that C14 has been taken up by other sinks. All of it? Or just part of it?
What you have left out is that C12 has also increased. CO2 in the atmosphere has increased by around 37% since the late 50’s. Almost all of it is C12.
So if DC14 has essentially returned to zero then
C14now/C12now = C14ref/C12ref.
But C12now = 1.37 * C12ref
Substituting
C14now/(1.37 * C14ref) = C14ref/C12 ref
Multiply both sides by 1.37 * C14ref
C14now = C14ref * 1.37
C14/C12 ratios may have reverted, but C14 quantities are still over 1/3rd higher nearly a ¾ of a century later.
The C14 data from the bomb pulse actually supports the IPCC position of a much longer Adjustment time.
Dear Glenn,
Thank you for your detailed comment. Your comment really applies to my (2019) paper. So, I pasted the relevant parts of my (2019) paper above because they answer most of your comments. Since my 11-slide presentation on this post is intended for non-scientists, I did not add all the detailed science that you discuss, If I had, it would have no longer been a simple presentation.
Section 3.3 of my (2019) paper derives the math necessary to explain how Te is fundamental to the physics. It shows how the level approaches the balance level set by the inflow. This uses outflow and inflow together properly, as you suggest should be done.
Figure 4 shows how the level approaches the balance level when outflow is combined with inflow. So far as I know, I am the only scientists who has properly defined the flows in the carbon cycle and calculated them. I don’t do handwaving. I do mathematical physics.
Section 6.1 of my (2019) paper illustrates what you are trying to say, but more clearly. E-time is the only meaningful time so far as physics is concerned. Adjustment time and Residence time have squishy definitions useful only for those who can’t understand the math of how e-time explains everything, as my math shows.
My Figure 10 in my slides above comes from Figure 12 in my (2023) paper. I had not figured out this explanation in 2019. But my (2023) paper finally provides the proper way to interpret the carbon-14 data. It answers your comments about carbon-14.
I think this answers all your comments. If not, please tell me.
I cannot check your debate. However, I think that one significant factor is missing from the analysis.
The ocean’s CO2 absorption is not determined by processes at the surface.
In the toposphere, the initially neutral vapour dissolves the CO2 content of the air as it becomes a cloud. For this reason, the pH of the rain produced in clean air is 5.6. http://nimbus.elte.hu/oktatasi_anyagok/levegokemia/13_Csapadekkemia.pdf “Precipitation Chemistry” Slide 15 “Precipitation around pH = 5.6 is “neutral” precipitation from the point of view of the atmosphere. Nature has adapted to this. (Slightly chemically acidic – natural acidity.)”
Water in the Earth’s atmosphere is exchanged every 10 days. https://edit.elte.hu/xmlui/bitstream/handle/10831/77732/EMF_2020_Evf32__09__Weidinger-Tasnadi.pdf?sequence=1 “Water in the atmosphere” p. 88.
This may be the reason why, despite considerable local variation in CO2 emissions, the distribution of CO2 in the air is relatively uniform.
However, the amount of dissolved gases in water is sensitive to warming. If the ocean warms, more CO2 will be in the air.
The water temperature in the Bermuda Triangle has risen by 1 degree C in 40 years. https://bios.asu.edu/currents/atlantic-ocean-near-bermuda-is-warmer-and-more-acidic-than-ever-40-years-of-observation-show/ Presumably due to an undersea volcano there.
And the frequency of volcanism, despite claims, has been increasing recently https://energmester.hu/klima/vulkanizmus/index_teljes.html