by Richard J. Petschauer (January 18, 2011)
1. Background
Climate science is certainly not settled considering how poorly the models handle latent heat transfer. This is a process involving heat loss on the surface from evaporation that is moved to a corresponding heat gain when condensation occurs during cloud formation, causing added heat to be radiated to outer space which helps cool the planet. Why is it now being treated poorly by the climate models?
We will show that the complex computer models greatly underestimate how much evaporation increases with surface temperature, and it is not clear how they treat even this amount of cooling. These computer models have been questioned lately for other reasons since certain observed data does not agree with the models’ estimates. The back-up to these complex models use simple energy balance concepts that at first glance appear correct. However the two main versions of these simple models completely ignore changes in this latent heat transfer, even the small amounts the complex models estimate.
There has been good data for over 10 years that shows this is a significant part of the heat that cools the surface as shown in global energy balance estimates. Well-tested basic physics equations show that this evaporation will increase rapidly with surface temperature. It will counteract warming from any cause including that from increased greenhouse gases.
We suspect that the reason the present simple models ignore the feedback role of evaporation is that the models only deal with heat transfers caused by radiation because this is the only way the heat enters and leaves the entire planet. In doing so however we believe the relationship between the temperature of the earth’s surface, the one we care about, and the amount of the outward emitting radiation is not handled correctly.
The present Radiation Forcing Theory places an overemphasis on radiation, resulting in a scientific blind spot. This paper presents a proposed method using an improved simple model to correct this oversight and provides new climate sensitivity estimates that are greatly reduced, even when using the low evaporation rates of the complex computer models.
2. Summary
This paper shows that the present radiation forcing theory methods are too simple and cause the climate sensitivity from increased CO2 to be substantially overestimated. Our analysis and corrections are based on a more complete picture of all the heat flows involved supported by well-documented existing published data, and how to estimate the amount evaporation cooling will reduce warming caused by increased CO2.
We evaluate the two main simple methods now being used to estimate the pre-feedback surface temperature increase from doubling of atmospheric CO2 content, the common benchmark for climate sensitivity. While there are some problems here, the major concern is in the next step of calculating feedback where these simple models ignore changes in evaporation heat transfer.
We also explain why we think the present complex computer models compound this problem and underestimate the rate surface water evaporation changes with temperature, and why proven equations should be used instead. Oceans provide most of the evaporation, and since their temperatures rise more slowly than that over land, much of this cooling feedback will be delayed to future years. The appendix provides ways to estimate the result under these conditions.
The IPCC central value estimate of the final temperature rise from CO2 doubling including all feedbacks is 3.26 C. Our new model using only the low evaporation rates of the complex computer models reduces it to 1.49 C. With expected evaporation changes of 6% / C, it drops to 0.79 C, or 0.69 C if questionable positive cloud feedback is eliminated.
3. Basis for the Methodology Used Here
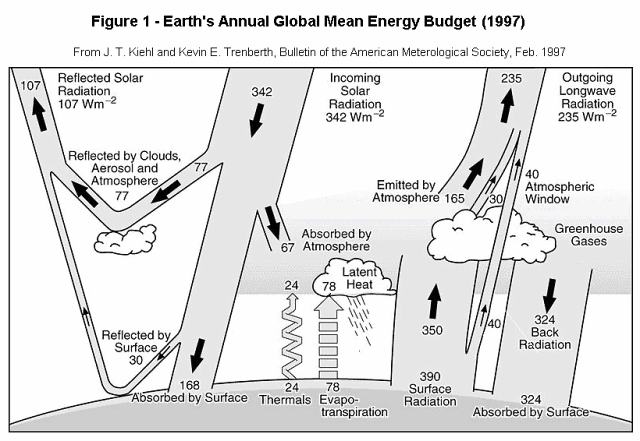
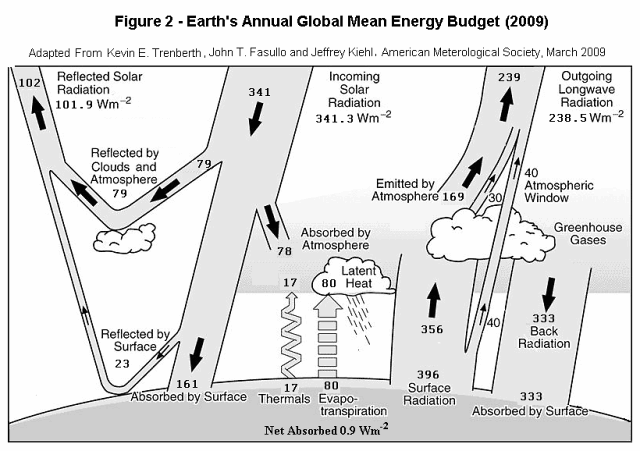
The primary basis for estimates made here regarding climate sensitivity to increased carbon dioxide in the atmosphere is the data from the Kiehl and Trenberth (1997) Earth’s Annual Global Mean Energy Budget (referred to here as the “1997 values”) shown in Figure 1 and an updated by Trenberth et al. (2009) shown in Figure 2 (the “2009 values”). Since Figure 1 has had a broad circulation, we will refer to it for most of the explanations. However the calculations are done for each set of values and the results are very close, indicating small sensitivity to the changes.
Difference Between Present Simple Models and Our Proposed Improved Simple Model
It is important to point out how little of the information in these energy budgets the present simple models actually use in their estimates. For this we will use the 1997 values from Figure 1 as an example. There are two main types of methods used. One type uses only the combined outgoing longwave flux of 235. The other type uses net incoming shortwave solar flux (342 – 107 = 235) and the estimated average global temperature (15 C) that sets the value of surface radiation (390). Both assume correctly that after a change, such as from more greenhouse gases reducing the outgoing flux, the temperatures of the atmosphere and the surface will change to bring the outgoing back in balance with the input. An estimate is made of how much the surface temperature will change in response to a perturbation or “forcing” of a 1 Wm-2 change in either the outgoing or incoming flux. The result is a “temperature sensitivity factor” in C / Wm-2 that relates how changes in net in/out fluxes from forcings or feedbacks alter surface temperatures.
One problem here is that no distinction is made between changes in incoming solar shortwave flux and infrared or longwave flux. We will show that the former has a significantly larger effect since the atmosphere absorbs much less of it compared to longwave radiation. The IPCC method uses the version based on solar changes and thereby overstates the temperature sensitivity factor with no feedback, which also increases the feedback multiplier. In our method we provide different temperature sensitivity factors for shortwave and longwave forcings.
A second problem in the present methods is that all forcings and feedbacks are referred to the top of the atmosphere (TOA). This does have the advantage in that satellite measurement data provides values here for both present incoming and outgoing flux that can also be used to verify greenhouse gas absorption calculations. But as can be seen from Figure 1 with the 78 Wm-2, the perturbation from a change in evaporation caused by a surface temperature change between the surface and the atmosphere, not at the TOA. Perhaps this is why these models have no estimates for changes in the evaporation.
In our method we use all the 1997 (or 2009) values and allow forcings and feedbacks at the TOA as well as other places, solve for balance not only at the top of the atmosphere, but also at the surface and the atmosphere itself and determine separate temperature sensitivity factors for each location and type of radiation. In the 1997 values, all three are already in balance before any forcings while there is a net unbalance of 0.9 Wm-2 at the surface in the 2009 values. For the 2009 values to balance, the surface radiation must increase to balance. The estimated new state of the values then forms the baseline for forcings and feedbacks.
4. Climate Sensitivity Before Feedback – Present Methods
We use the normal definition of “climate sensitivity” as the change in surface temperature for a doubling of atmospheric CO2 after the climate system adjusts and comes into a new equilibrium state. (Most estimates indicate that the temperature change follows an approximate logarithmic function with CO2 changes, hence any doubling will cause about the same temperature change.) At this time most of the uncertainty is in the secondary response, or “feedbacks” from the initial temperature change from the CO2. An important feedback is from water vapor, a strong greenhouse gas, since warmer air usually holds more of it. There are two basic present methods mostly used for the pre-feedback climate sensitivity. Both use forcing at the TOA defined by an empirical equation based of changes of outgoing longwave flux as 5.35 ln (Cx/Co). For two times CO2 this gives a 3.71 Wm-2 decrease. So the planet including the atmosphere must increase in temperature and outgoing radiation to compensate for this in order to balance an unchanged incoming solar energy.
4a. First Present Method
The first present method uses only the estimated value of outgoing longwave radiation, 235 Wm-2 shown in Figure 1, and tries to determine if this value changes by 1 Wm-2 how much the surface temperature must change so the outgoing flux changes so it remains in balance with the input of net 235 Wm-2 (342 – 107). It does this by estimating a temperature change of the atmosphere and clouds needed for this and assumes the surface temperature will change the same amount even though there is not much coupling directly from the surface to outer space. The required temperature change of the atmosphere and clouds can be determined by using the Stefan-Boltzmann radiation equation. The first derivative of this equation is the rate of change of the radiation with temperature. The reciprocal of this is defined as the temperature sensitivity factor, k. It is the change in temperature in degrees Celsius needed to produce (or associated with) a 1 Wm-2 change of radiation.
The radiated flux from Stefan-Boltzmann where s = 5.67e-8 and e = the emissivity constant,
(1) W = seT 4
(2) dW/dT = 4seT 3
Where W is in Wm-2 and T is in degrees Kelvin.
By inverting and using substitutions, there are three forms of the temperature sensitivity factor.
(3) k = dT/d W = 1 / (4seT 3) = 1 / (4s 0.25 e 0.25 W 0.75) = T / 4W
Note the last form is independent of e, but only if T and W are known.
Using the second form for a typical assumption of e = 1 and a flux of 235 Wm-2, gives a value of 0.270 C / Wm-2 for k. For a forcing of 3.71 Wm-2 for 2x CO2, this gives pre feedback values of 1.00 C temperature increase. This is the value of the clouds and atmosphere will change. A significant and questionable assumption of this method is that the surface temperature will change the same amount as the atmosphere that produces the new value of outgoing radiation. This assumption may be invalid due to shielding from clouds that can reduce the surface temperature change compared to that of the upper atmosphere for incoming changes in flux. This is now handled by a negative lapse rate feedback. However significant increases in non-radiative heat leaving the surface such as from evaporation are ignored. This would reduce the amount the surface temperature need to increase and should be considered as feedback since it is caused by a change in surface temperature. As an alternative, the value of k could be corrected.
4b. Second Present Method
A second common method, which according to Monckton (2008) is from Kiehl (1992) and seems to be used by the IPCC (implied from their estimates of climate sensitivity). It is based on additional data, namely the estimated present mean global surface temperature of 15 C (based on the 1997 values) combined with a net incoming shortwave radiation that is in balance with the outgoing longwave radiation of 235 Wm-2. With a surface emissivity of 1 this corresponds to an outgoing surface radiation of 390 Wm-2 as shown in Figure 1. This method assumes if the net input solar heat increases by 1%, for example, the radiation of 390 Wm-2 will also increase by the same relative amount, in this case 1%. Implicit in the method (although not stated) is what this writer calls the greenhouse multiplying effect, or simply a “greenhouse multiplier” in that 235 Wm-2 of incoming radiation produces a temperature at the surface of 390 Wm-2, a multiplier of 1.66. (Conversely, one can think of the 390 Wm-2 leaving the surface, the greenhouse effect attenuates it by a factor of 1.66, so that only 235 Wm-2 escapes to outer space). If we use the above equation for ko at the surface we get 0.1846 C / Wm-2. Then this times 1.66 gives a value for k of 0.306 Wm-2, about 30% higher than the first method. This has also been calculated directly by some by using the third equation for k, T / 4W or 288/(4 x 235). However this is not a correct use of the radiation equation since the values for T and W are from different locations. A forcing of 3.71 Wm-2 for 2x CO2 gives a pre-feedback value of l of 1.14 C, close to that used by IPCC of 1.13 that corresponding to 236 Wm-2 that they use for outgoing longwave radiation.
Note two significant implied assumptions here:
(1) Additional changes in forcing will have the same temperature sensitivity factor as the average of all those up to the present state. However since water vapor increases with temperature, and must have up until the present time, it appears that a major portion of the water vapor feedback may be already included in k using this method. Also we will show that this method applies only to changes in solar shortwave forcings.
(2) All of the heat transfers in Figure 1 change in the same proportion as the change in net incoming flux. From this it can be shown using the radiation equation that the surface outgoing radiation will increase 1.39% / C. So this method includes this small increase in evaporation, but still much less than expected at about 6% / C. But the net value of 0.306 is still higher than that of the first method. Later we show that if the evaporation Figure 1 is held constant, the values rises to 0.355 C / Wm-2 for solar forcing.
4c. Additional Problems with Both Present Methods
Besides the simple assumptions of the present methods mentioned above, the energy balance of Figure 1 shows two significant additional errors. The first one can be seen from the expectation that the temperature response to forcing should be bi-directional. That is, increases and decreases of forcing of the same magnitude will cause equal temperature changes, but of the opposite direction. It follows then that a decrease in outgoing radiation should cause the same temperature increase as an increase in incoming radiation of the same amount. If we now estimate climate sensitivity by the temperature increase due to a hypothetical increase in an external longwave source, it can be seen from Figure 1 that surface temperature increase will be much less compared to the same forcing from solar shortwave radiation since the atmosphere will attenuate nearly all of the longwave absorption whereas for the case of solar flux 168 out of 235 Wm-2 or about 71% strikes the surface directly.
So changes in net shortwave incoming compared to changes in longwave outgoing of the same amount of Wm-2 will cause significantly larger surface temperature changes.
This has a larger effect on the second or IPCC method yielding a temperature sensitivity factor or 0.306 since it is based on the relation of present surface temperature to the net incoming solar energy that produces it. It also affects the first method since incoming longwave radiation should increase the temperature of the atmosphere more than the surface especially the cloud tops, with less flux reaching the surface. From the visual standpoint, the role of clouds in Figure 1 appears to be much less than the value 62% combined cloud cover at three levels used in the 1997 values. This is because much of the radiation leaving the clouds, either up or down is intercepted and re-radiated by the greenhouse gases. However clouds, except for the very high ones, are opaque to longwave radiation and have emissivity values close to 1. Figure 1 could be redone to better depict this, although the net flux flows leaving the planet would not change. It also follows that any change in clouds that affects the amount of net solar energy reaching the surface will have a greater temperature sensitivity factor than that from greenhouse gases.
There is another subtle difference between solar forcing and that due to increased greenhouse absorption. With a change in net incoming solar flux, the forcing remains after rebalancing is complete. With changes in CO2 concentrations however, the forcing is reduced to zero after the new state is in place. In some other systems under these conditions, the second type produces less change than the first type for the same amount of initial forcing. It is not obvious which way the climate system works, but the present theory treats the two types of forcings in the same way.
4d. Negative Lapse Rate Feedback
Part of what this paper points out as additional problems outlined above with the present methods is now compensated by a negative feedback from the lapse rate. This is to compensate for the upper atmosphere warming more than the surface as alluded to here. Monckton (2008) reports according to Soden and Held (2006) the IPCC’s value for this is – 0.84 Wm-2 / C. The feedback multiplier for this with no other feedback gives 1 / (1 + 0.84 * 0.270) or 0.851 for method 1 and 1 / (1 + 0.84 * 0.306) or 0.796 for method 2. We believe the method used here that solves directly for a new energy balance state is superior and is a closer representation of the actual climate system, but also requires a correction. But as of now we do not have a method to estimate it, so we will use the present lapse rate feedback estimate. More discussion on this later.
4e. Does Lapse Rate Already Account for Evaporation Feedback?
We have seen comments on the Internet that claim that the lapse rate already accounts for warming from latent heat release. Yes, but not for changes in it from increased evaporations. The lapse rate is different from what would happen if only the pressure drop with altitude is considered according to the gas laws. The atmosphere cools less with altitude than estimated from gas laws because heating from convection from the surface, absorption of shortwave and longwave radiation and latent heat release when water vapor condenses to form clouds. While surface evaporation will cool the surface and reduce upward convection, the corresponding latent heat release will occur at higher altitudes and tend to increase the faction of atmospheric outgoing radiation in the upward direction. So the present lapse rate is a function of these warmings and not the cause of it. The lapse rate is not an independent variable, but a dependent one.
5. Climate Sensitivity Before Feedback – Full Energy Balance Method
One of the present methods described above considers only the outgoing planet radiation and the second method adds the present surface radiation implied from the temperature. The new method proposed here uses all the values shown in Figure 1, calculates an initial equilibrium state, perturbs any one or more values and finds a new equilibrium state for all the values and a resulting surface temperature change. While the values in Figure 1 are in balance already, this is not necessary for this method. Additional details are provided in the appendix. The key points are covered here.
In using the new energy balance method for net solar or CO2 forcing, we stay with the present concept with forcing at the top of the atmosphere (TOA) and estimate the surface temperature change for a 1 Wm-2 decrease in outgoing longwave radiation at the top of the atmosphere. This provides k, the temperature sensitivity factor that is then multiplied by the 3.71 Wm-2 forcing commonly estimated for 2x CO2. We create this forcing by using a perturbation and solve the simultaneous equations that balance the flux flows in and out of the surface, the atmosphere and the entire planet. There is only one solution which is the new equilibrium states for all the values shown in Figure 1. The new outgoing surface radiation defines the new surface temperature using the radiation equation. We use the Matlabâ software matrix algebra function that provides the solution to N linear equations of N unknowns. A separate program checks for balance at the three levels.
In order to stay with the present convention for the cases which do not involve feedback, we change the convection and evaporation fluxes in Figure 1, now at 24 and 78 Wm-2 in the same relative proportion as the surface radiation which is about 1.39% / C since this matches the assumption in present method 2 used by the IPCC. We do not include this amount as feedback, only values above it. We first run the equations with the initial values to determine the balanced state and the surface radiation. For the values of Figure 1, which are already in balance, it gives 390 Wm-2 shown for which we calculate a temperature of 14.9853 C. For the 2009 values there is an unbalance of 0.9 Wm-2 and the balanced surface radiation is estimated at 397.8668 Wm-2 implying 16.4267 C.
We first run a case with a perturbation of a 1 Wm-2 solar forcing at the TOA while keeping the relative fractions of the two albedos and the atmosphere absorptions unchanged and the fraction of the shortwave absorption (initially at 67 Wm-2 in Figure 1). The solution gives a surface radiation after balance of 391.6594 Wm-2 implying a temperature rise of 0.3058 C equivalent to the IPCC value for k of 0.306 Wm-2, verifying the present method 2 for shortwave forcing without feedback.
Key factors in these runs keeps the ratio of the downward and upward atmosphere radiations unchanged (324 and 195 Wm-2 in Figure 1) and the fraction of the surface radiation that escapes through the atmospheric window (40/390).
The next step was to run the temperature change for a 1 Wm-2 longwave forcing from greenhouse gases at the TOA. This was done in three different ways. First, the ratio of the outgoing radiation to the downward was changed from to 195/324 to 194/324 (we actually use the “downwelling fraction” of 324 / (324 + 195) which increases to 324 / (324 + 194). In the second way the fraction of the radiation through the atmospheric window was cut from 40/390 to 39/390, and in the third way the amount of the solar atmosphere absorption was increased from 67 to 68 Wm-2 without changing that striking the surface or reflected from it. The resulting surface temperature changes for new equilibrium states were as follows:
Increase downwelling fraction 1 Wm-2 : DT = + 0.2149 C
Decrease flux through window 1 Wm-2 : DT = + 0.2146 C
Increase atmosphere absorption 1 Wm-2 : DT = + 0.2139 C
These are all very close and forcing at the TOA of about 0.215 C / Wm-2, considerably less the present methods ranging from 0.270 to 0.306. The corresponding temperature increase from 2x CO2 before feedback becomes 3.71 x 0.215 or 0.80 C compared with a range of 1.0 to 1.14 using the present methods. Note that in the present method of referring all feedback factors to the TOA, a reduced value of k also reduces the feedback which is the feedback factor times k.
The results for the above second method in Wm-2 are shown with the changes in ( ).
G: 391.1637 (+1.1637),
D: 325.4682 (+1.4682),
U: 195.8836 (+0.8836),
W: 39.1164 (-0.8836),
E and Th: 102.3045 (+0.3045) and
T = 15.1999 (+0.2146 C) (up from 14.9853 C).
Where the radiations are G = surface, D = atmosphere down, U = atmosphere up, W = window, E & Th = evaporation plus thermals and T = surface temperature.
Note that the sum of the increases in G of 1.1637 and E/T of 0.3045 equal the increase in D of 1.4682, and the sum of U and W still add to 235, the net incoming short wave radiation, and W / G is changed from the base line values of 40 / 390 to 39 / 390 and E+Th increased by the same ratio as G. Also the relationship of U and D remain the same since the new values of U / D = 195 / 324.
There is a question whether the equilibrium process will further change the ratio of outgoing to downgoing atmosphere radiation. We think for longwave forcing at the TOA it will increase the fraction of radiation that is outgoing, thus reducing the surface temperature change, but have not quantified this nor include it in our estimates, but use the present lapse rate change estimates instead. If we did know how much it should change, we could estimate the related change in surface temperature by modifying the downwelling ratio to match it. We can look at how much the model estimates the temperature changes at the upper and lower levels by multiplying each flux change by its corresponding temperature sensitivity factor as calculated from the radiation equations using the initial flux values of 195 and 324 Wm-2. For the case above this gives an upper outgoing atmosphere level an increase of 0.274 C and 0.311 C for the lower downwelling location. A slight adjustment in the downwelling ratio from 0.624277 (the required value to balance to present values in Figure 1) to 0.624150 made them nearly equal at 0.2783 C and 0.2782 C and reduced the surface temperature rise from 0.2146 C to 0.1918 C. So if we knew from other sources the expected relative changes at the upper and lower atmosphere locations or at the surface, we could improve the estimates.
This new model can also be used to estimate the effect of other changes. Regarding changes in cloud cover, the net entering the atmosphere is changed, but also the amount absorbed by the atmosphere, which is partly from clouds. The appendix covers ways to separate these two effects.
6. Surface Evaporation Feedback
Figure 1 shows that the latent heat from evaporation is estimated at 78 Wm-2 and thermal convection of 24 Wm-2, a significant combined value of 102 Wm-2. Present method 1 assumes these do not change with temperature, and only the surface radiation rises to equal that of what is required to make up the loss at the outer atmosphere. The second method assumes they change in the same proportion as the surface radiation, which is about 1.39% / C since the premise is that everything changes in proportion to the net incoming solar flux. If method 1 used the same assumption, the surface radiation would be reduced by the amount the evaporation and thermals increase in order to keep the combined flux unchanged. Under this condition, the surface radiation change will drop by the factor 390 / (390 + 102) or 0.793. The temperature change will drop by the same fraction as the surface radiation or from 0.270 to 0.214 C / Wm-2. It is interesting that this value is nearly identical to 0.215 C / Wm-2, our estimate using our new energy balance method that also uses the same 1.39% / C evaporation rate change as the pre-feedback estimate. (Later we show how to use this simple method with other evaporation change rates). This is a significant drop showing the importance of these two non-radiative heat transfers even at a low rate of change. However we believe the actual increase is closer to 6% / C, and we treat the amount above 1.39% as negative feedback. If we assume no change in thermals or evaporation we get 0.260 C / Wm-2 in our model, close to the 0.270 of method 1. So it appears that present method 1 regarding longwave forcing is superior to method 2 as used by the IPCC.
6a. Using the Energy Balance Model to Estimate Evaporation Negative Feedback
The appendix discusses the implications of conditions of constantly increasing radiative forcing causing land temperatures to rise faster than those of the sea surface which produces most of the evaporation. The result is that some of the evaporation negative feedback is first attenuated and then delayed. Here we consider the simpler situation according to the usual definition of climate sensitivity which is the final equilibrium temperature change after a one-time change in forcing, including the effects of feedbacks, and assume both land and sea surface temperatures finally change the same amount, the usual convention.
The appendix covers reasons why we reject the complex computer model estimates of low evaporation rate changes compared to the expected value of about 6% / C. The short answer is when observed satellite data from Wentz et al. 2007) over 11 years supports equations that are based on well tested physics theory, one should not accept substantially different results from a computer model just because it is complicated. And these proven equations are based on water vapor partial pressure as a function of temperature that has been measured very accurately in labs for many years. The complex computer climate models are run with a constantly changing forcing simulating increasing atmospheric CO2 and we suspect the sea surface temperatures were not allowed enough time to warm to their final state compared to warmer air over land. Water temperature is the primary driver of evaporation; warmer air reduces it. A surface water temperature increase of 25% less than the air above will cut the evaporation increase in half. Or perhaps evaporation over land was not increased with temperature as it should since even with constant rainfall from the oceans, a larger fraction will be evaporated and recycled with less running off or soaking into the soil. In some models, relative humidity increases with temperature, contrary to data, that will reduce evaporation.
We should also point out that the actual rate of change of the evaporation for climate change purposes assumes that the warmer air will hold more water vapor such that the relative humidity (RH) will be constant. The same equations show the water vapor will increase the same approximate 6% / C. Some climate models have been reported constant RH in the atmosphere, while some shows it increasing. For evaporation purposes, the RH at the surface is controlling. Some mean historical data from mid-continent U. S. of different latitudes show surface RH drops at about 0.5% / C and more in the summer months. The estimate of the evaporation rate increase at a mean ocean surface temperature of 17 C at constant RH is about 6.5% / C. For a RH dropping 0.5% / C, it goes up to about 7.5% / C. So using a value of 6% seems conservative and allows for the fact that the final temperature rise in the ocean may take very long.
The equations that define the changes in the heat transfers after a perturbation were modified so that the evaporation of Figure 1, starting at 78 Wm-2, would vary with the surface temperature which was estimated from the change in surface radiation. We used one of four rates of change / C relative the surface temperature: 0, 1.39%, 2.5% and 6%. Since the surface radiation (at 15 C) changes 1.39% / C, we define feedback by the amount the evaporation change rate that exceeds this. In all cases we vary the thermals from the initial value of 24 Wm-2 by 1.39% / C consistent with the assumptions of the present method 2 used by the IPCC.
The results are shown in Table 1 for the four values of evaporation rate change with four types of forcings using both the 1997 data from Figure 1 and the 2009 updated data from Figure 2. It shows the surface temperature change for a 1 Wm-2 forcing. Note in column 2 and 4 the values for 1.39% shown in bold of 0.306 C and 0.215 C corresponding to the results described earlier for solar forcing and longwave forcing at the TOA. High atmosphere forcing is at the TOA. Low atmosphere forcing is for perturbations closer to the surface such as those from thermal or evaporation changes. These were determined by two ways with essentially the same results: A change in evaporation by 1
Table 1 – Surface Temperature Changes (C) Using Kiehl et al. 1997 and 2009 Energy Balance Baselines (Column 2 Forcing is Shortwave, Columns 3 to 5 are Longwave)
| Evaporation Change Rate
% / C | Net Solar
1 Wm-2 Forcing 1997 / 2009 | Low Atmosphere
1 Wm-2 Forcing 1997 / 2009 | High Atmosphere
1 Wm-2 Forcing 1997 / 2009 | High Atmosphere
4 Wm-2 Forcing 1997 / 2009 |
| 0 | 0.355 / 0.352 | 0.150 / 0.150 | 0.250 / 0.253 | 1.008 / 1.021 |
| 1.39% | 0.306 / 0.302 | 0.129 / 0.129 | 0.215 / 0.217 | 0.869 / 0.877 |
| 2.5% | 0.275 / 0.271 | 0.116 / 0.116 | 0.193 / 0.195 | 0.782 / 0.787 |
| 6% | 0.209 / 0.205 | 0.088 / 0.087 | 0.147 / 0.147 | 0.595 / 0.596 |
Wm-2 or a change in the downwelling ratio to 325 / (325 + 195). Note the results for both data sets are quite close. The values for the 2009 data are somewhat lower because the higher surface radiation and surface temperature produce lower temperature sensitivity factors based on the radiation equation.
6b. First Method to Estimate Evaporation Feedback
There are two ways to estimate the water vapor feedback from this data. The first way provides the feedback multiplier directly since the values are after equilibrium is reached. For the 6% case, each 6% value is divided by the corresponding 1.39% value which equals the feedback multiplier.
From Table 1, we will use the 2009 data as more current. For each of the four columns we divide the values in the fourth row by those in the second row, we get 0.679, 0.674, 0.677, and 0.680. Since the last value is close to the forcing for 2x CO2 we will use it, 0.680. Solving the feedback multiplier equation for the feedback fraction we get for the 6% / C evaporation rate change,
(4) f = (m – 1) / m = (0.680 – 1) / 0.680 = –0.471 C / C
This is the value that can be combined with fractions from other feedbacks. For comparison from Monckton (2008) the IPCC value for water vapor is +1.8 x 0.305 or + 0.549 C / C and for the lapse rate –0.84 x 0.305 or –0.256 C / C. However since both involve longwave feedback referred to the TOA, we feel the correct value of k is 0.215 not 0.305 which reduces these feedbacks to +1.8 x 0.215 or 0.387 C / C and –0.84 x 0.215 or –0.181 C / C. Note now that negative evaporation feedback at a 6% / C change rate is more than enough to offset positive water vapor feedback using IPCC values for the feedback factor of 1.8 Wm-2 / C.
6c. Second Method to Estimate Evaporation Feedback Using the Perturbation Forcing Method
The method starts with the present evaporation value. We will use the more recent 2009 value of 80 Wm-2. Assume something caused a 1 C rise in surface temperature. The simple model assumes that the evaporation 80 Wm-2 would rise 1.39%. But if it actually increases 6%, this gives an additional cooling perturbation forcing at the lower atmosphere of (6 –1.39) / 100 x 80 or 3.688 Wm-2. Multiplying this by the temperature sensitivity factor at the lower atmosphere at the 1.39% rate of 0.129 C / Wm-2 from Table 1 gives a temperature change of –0.476 C, the feedback value since we started with a surface temperature change of 1 C. This is close to the value of –0.471 C estimated with the first method. This shows an approximate linear relationship between the “excess” evaporation rate and the feedback fraction. A simple way to estimate it for different values of R, the evaporation percent change rate per C, is:
(5) f = – (R – 1.39) / 100 x 80 x 0.129 = –0.1032 (R – 1.39)
For a change rate of 6.5% / C for example, this gives –0.527 C / C.
6d. Does Increased Evaporation Change the Downwelling Fraction?
Central to our method used here is a fixed ratio of flux leaving the atmosphere going to the surface to the total leaving the atmosphere, unless the perturbation is a change in this ratio. We think of changes in the fraction caused by the balancing process as additional feedback, similar to the lapse rate feedback presently used. The model itself can give this change if we know how the downwelling fraction changes. At this time we have no way of doing this except in a qualitative way that judges if the fraction increases or decreases. The former will increase the surface temperature, the latter decrease it. For the case of a forcing of increased downward flux at the TOA we think the outgoing fraction will increase causing added cooling so our estimate gives a lower bound of the final temperature rise. For the case of evaporation cooling we think that the heat transferred when the water vapor condenses will be at a higher altitude than where the typical longwave radiation from the surface is absorbed that we estimate from other work at about 50% by 1 km. This will decrease the downwelling ratio and increase the magnitude of the negative feedback, so we think our estimate is conservative.
6e. Alternate Simple Approximation of Evaporation Feedback
We can generalize the earlier approximate calculations we used for present method 1. It assumes the temperature change at the surface will equal that at upper atmosphere that is needed to balance a change the forcing that is estimated at 0.270 C / Wm-2. However according to this simple concept, all that has to happen is that the same amount of longwave flux change must occur from the surface to the atmosphere. Since the higher surface temperature reduces its temperature sensitivity factor from that at the emission level of the atmosphere, the flux change at the surface must increase by a factor of 0.270 / 0.1846 or 1.463 higher (at a 15 C surface temperature). The rate at the surface is 1 / 0.1846 or 5.416 Wm-2 / C or 5.416 / 390 = 1.39% / C. If we assume that thermals change at the same rate as surface radiation and evaporation changes exponentially at R% / C, evaporation flux will change for small temperature changes as approximately R/100 x 80 x DT using the 2009 values. So a 1 Wm-2 forcing at the TOA requires a flux change leaving the surface 1.463 times larger which corresponds to a temperature change DT where
(6) 5.416 DT + (0.0139 x 17) DT + 0.8 RDT = 1.463
So
(7) DT = 1.463 / (5.416 + 0.236 + 0.8R)
For R = 0, 1.3%, 2.5% and 6% we get as approximations of DT as 0.259, 0.216, 0.191 and 0.140 C.
These compare with the 2009 values column four of Table 1 of 0.253, 0.215, 0.193 and 0.147 C
7. Estimating New Climate Sensitivity Values
Based on our revised estimates of climate sensitivity and considering evaporation feedback we will compare our revised climate sensitivity feedbacks with those of the IPCC before and after all feedbacks. All values are central value (most likely) estimates.
7a. IPCC Estimate
Before feedback.
(8) k = 0.305 C / Wm-2 (method 2);
forcing
(9) w/ 2x CO2 = 5.35 ln(2) = 3.708 Wm-2
(10) DT = 0.305 x 3.708 = 1.13 C
Feedback factors (per Monckton (2008) referencing Soden and Held (2006), all values in Wm-2 / C:
Water vapor = +1.8;
Lapse rate = -0.84;
Clouds = +0.69;
surface albedo = 0.26;
CO2 = 0.25.
Total feedback factors = 1.8 – 0.84 + 0.69 + 0.26 + 0.25 = 2.16 Wm-2 / C
Total feedback = 2.16 x 0.305 = 0.6588 C / C
After feedback (our estimate of IPCC method):
(11) DT = 1.13 / (1 – 0.6588) = 3.31 C
Actual value from IPCC 2007 = 3.26 C
7b. New Method with Evaporation at only 1.39% / C – Similar to Complex Climate Models
Before feedback, from Table 1, for forcing at top of atmosphere at base line
(12) r = 1.39%, k = 0.215
(13) DT = 0.215 x 3.708 = 0.797 C
Feedback using IPCC feedback factors and k = 0.215
(14) F = 2.16 x 0.215 = 0.4644 / C
(15) DT = 0.797 / (1 – 0.4644) = 1.49 C
7c. New Method with Full Evaporation Feedback at 6% / C
Before feedback, from Table 1, for forcing at top of atmosphere at base line
(16) r = 1.39%, k = 0.215
(17) DT = 0.215 x 3.708 = 0.797 C
Total Feedback using IPCC feedback factors with revised k combined with evaporation feedback at 6 / C rate and feedback of – 0.471 C / C.
(18) Total feedback = 2.16 x 0.215 – 0.476 = – 0.0066 C / C
(19) DT = 0.797 / (1 – (– 0.0066 )) = 0.792 C
7d. New Method as Above but with Zero Cloud Feedback
Roy Spencer has presented reasons why cloud feedback may be negative. If we just assume it is zero, and recalculate the above with it removed,
(20) Total feedback = 2.16 x 0.215 – 0.69 x 0.215 – 0.476 = – 0.1550 C / C
(21) DT = 0.797 / (1 – (– 0.1550 )) = 0.690 C
7e. New Method as Above but with Negative Cloud Feedback
If we let the cloud feedback be negative of the same amount and recalculate the above,
(22) Total feedback = 2.16 x 0.215 – 2 x 0.69 x 0.215 – 0.476 = – 0.3033 C / C
(23) DT = 0.797 / (1 – (– 0.3033 )) = 0.612 C
Table 3 shows the results. The second row uses the 1.39% evaporation change rate, typical of the complex computer models, and cuts the IPCC estimate by over 50%. Using a full evaporation rate of 6% / C in the third row cuts it about 75%.
Table 3 – Comparison of Climate Sensitivity Estimates (Temperature Rise for CO2 Doubling) of Present IPCC Values with New Methods, Evaporation Feedback and Various Cloud Feedbacks. All Values are Central Value (Most Likely) Estimates
|
Case | Temp Sens. Factor
k (C / Wm-2) | DT With No
Feedback (C) |
Feedback (C / C) | DT With Feedback (C) |
| Present IPCC
Method | 0.305 | 1.13 | 0.6588 | 3.31 or
3.26 per IPCC |
| Correct k for Longwave | 0.215 | 0.797 | 0.4644 | 1.49 |
| Add Full Evap.
Feedback | 0.215 | 0.797 | – 0.0066 | 0.792 |
| Change Cloud Feedback to 0 | 0.215 | 0.797 | – 0.1550 | 0.690 |
| Cloud Feedback Negative | 0.215 | 0.797 | – 0.3033 | 0.612 |
The range of the IPCC estimates is 2 C to 4.5 C. Using the IPCC method, the 4.5 C value requires a feedback value to increase from 2.16 to 2.473, an increase of about 15%. If we use that value and decrease our estimate of the negative feedback of – 0.476 C / C by 15% to get an approximate estimate of a statistical upper bound, and use our value of k of 0.215, the result is 0.913 C.
(24) Total feedback = 2.473 x 0.215 – 0.476 x 0.85 = + 0.127 C / C
(25) DT = 0.797 / (1 – 0.127) = 0.913 C
Doing a similar calculation on the lower limit results in a value of 0.645 C.
7f. Effect of Sea Surface Temperature Delays
The thermal inertia of the ocean is much more complicated than land because of complex mixing between layers which can vary in depths for various ocean locations, and it is beyond the scope of this paper to estimate it. The ocean thermal delays are considerably longer than those of land. As explained in more detail in the appendix, simulations done by the writer for distributed heat flow and storage in 200 meters of soil with a ramp function of forcing (constant increase with time), the surface temperature is about 80% of the value corresponding to that of zero delay after 1 year, 95% after 10 years and over 98% after 100 years. As a typical example we will assume a sea surface temperature delay 10 times that of the land. The results are shown in Table 4 for a final evaporation increase rate of 6.28% / C. We assume for the sea, the air surface and water surface temperatures change together with constant RH and ignore air mixing between land and sea air temperatures.
Table 4 – Sea Divided by Land Surface Temperature Rises vs. Time with Ocean Surface Delay 10X Land Delay and Effect on Evaporation Rate Increase
| Year | 1 | 3 | 10 | 20 | 30 | 100 |
| Sea / Land Temperature Rise | 0.42 | 0.67 | 0.80 | 0.90 | 0.92 | 0.96 |
| Evaporation Rate Increase – % / C | 3.17 | 4.50 | 5.20 | 5.74 | 5.85 | 6.0 |
8. Conclusions and Recommendations
We have shown an improved simple method that uses data representing the mean global energy budget to estimate climate sensitivity including negative feedback from evaporation latent heat transfer that has been ignored by the present simple models. Using the complex computer models’
estimates of evaporation changes with temperature, that what we think are low, the IPCC climate sensitivity is reduced by over 50%, and about 75% if the evaporation rate changes follow expected equations and measured data. While the lag of ocean temperature changes will delay some of this feedback, significant effects should already be in progress since CO2 increases started many decades ago. Additional work regarding the temperature increase of the atmosphere vs. altitude caused by increased CO2 for clear skies and various cases of clouds would provide values that could be used to improve the estimation methods proposed here. Computer simulations using downward longwave forcing from the top of the atmosphere at the wavelengths caused by CO2 doubling, which are at two narrow bands one around 15 and 18 microns where the absorption widening occurs might be a simpler way to do this.
9. References
Kiehl, J. T., and K. E. Trenberth (1997): Earth’s Annual Global Mean Energy Budget. Bull. Amer. Meteorol. Soc., 78: 197-208
Kiehl, J.T. (1992) Atmospheric general circulation modeling, in Climate System Modeling, ed.
Mitchell, J. F. B., C. A. Wilson and W. M. Cunnington: (1987) On CO2 climate sensitivity and model dependence of results. Q. J. R. Meteorol. Soc. 113, pp. 293-322
Monckton, Christopher (2008), Climate Sensitivity Reconsidered, APS Physics Newsletters
Soden, B.J., and Held, I.M. (2006) An assessment of climate feedbacks in coupled ocean-atmosphere models. J. Clim.19: 3354–3360.
Trenberth, K. E., Fasullo, J. T. and J. T. Kiehl (2009): Earth’s Global Energy Budget, Am. Meteorol. Society, March 2009
Wentz, F. J., L. Ricciardulli, K. Hilburn and C. Mears: (2007) How much more rain will global warming bring? Science, Vol 317, 13 July 2007, pp. 233-235
_______________________________________________
Appendix and Supporting Material for
Climate Science’s Blind Spot – Evaporation Cooling
(Note: Figure 1 and 2 refer to those in the main paper)
A1. Model Results
We used three methods to simulate 1 Wm-2 of longwave forcing. The first one reduced the outgoing atmosphere radiation by 1 Wm-2, changing the ratio of outgoing to downward radiation and holding at this altered condition. The second method increased the atmospheric absorption by 1 Wm-2, but kept the net arriving at the surface at 168 Wm-2. The third method reduced the amount of radiation going directly from the surface to outer space from 40 to 39 Wm-2. The results of the surface temperature rises for the three were respectively, 0.2149 C, 0.2139 C, and 0.2146 C, being nearly equal. When using the 2009 data that is not shown here, the increases went up about 1% to 0.2169, 0.2153 and 0.2170 C.
Using the data from Kiehl and Trenberth in either Figure 1 (the 1997 data) or Figure 2 (the 2009 data), the model first establishes a baseline using the solar input, albedo and absorption fractions, thermal and evaporation fluxes, fraction escaping from the surface to outer space and fraction of the atmosphere radiation leaving it that strikes the surface or 324/(324+195) for the 1997 data or 333/(333 + 199) for the 2009 data. Using Matlab’s linear matrix algebra (Numerical Recipes routine GaussJ is an alternative), the model solves the simultaneous equations for the surface radiation, and the downward and outward radiation fluxes that balance the heat flux at the three levels: the surface, the atmosphere, and the planet. The surface temperature is calculated from the surface radiation using the Stefan-Boltzmann equation using a surface emissivity of 1.
Running the baseline data for the 1997 data gives the exact values for the three radiations, that are 390, 324 and 195 Wm-2 and a surface temperature of 14.9853 C. We then run with the new values and determine the temperature change based on the new balance solution. The 2009 data is not balanced as seen in Figure 2 where there is a net 0.9 Wm-2 being absorbed by the surface. The results of this are discussed later.
We used three methods to simulate 1 Wm-2 of longwave forcing. The first method reduced the outgoing atmosphere radiation by 1 Wm-2, changing the ratio of outgoing to downward radiation and holding it at this altered condition. The second method increased the atmospheric absorption by 1 Wm-2, but kept the net arriving at the surface at 168 Wm-2. The third method reduced the amount of radiation going directly from the surface to outer space from 40 to 39 Wm-2. The results of the surface temperature rises using the 1997 data for the three were respectively, 0.2149 C, 0.2139 C, and 0.2146 C, which are nearly equal. When using the 2009 data, the increases went up about 1% to 0.2169, 0.2153 and 0.2170 C.
These are the detailed outputs using the 1997 data for the first method of reducing the outgoing radiation 1 Wm-2 from 195 to 194 which means the downward fraction becomes 324/(324 + 194).
Where the radiations are G = surface, D = atmosphere down, U = atmosphere up, W = window, E/Th = evaporation plus thermals and T = surface temperature.
The results in Wm-2 are shown with the changes in ( ).
G: 391.1655 (+1.1655),
D: 325.4705 (+1.4705),
U: 194.8805 (-0.1195),
W: 40.1195 (+0.1195),
E/Th: 102.3050 (+0.3050) and
DT = +0.2149 C (up from 14.9853).
Note that the sum of the increases in the outgoing surface fluxes of G of 1.1655 and E/Th of 0.3050, equals the increase in downwelling, D, of 1.4705; the sum of U and W still add to 235, equaling the net incoming short wave radiation; the ratio W / G is unchanged from the baseline values of 40 / 390. Also D / (U + D) has the same value as 324 / (324 + 194) or 0.6254826; and that G and E+Th both increased by the same amount, 0.299% or 1.39% / C.
Also note the “greenhouse multiplier” is only 1.1655, much less than 1.66 incorrectly used by the IPCC method. This is the only solution for the given change, which in this case changed the downwelling fraction from 324/(324 + 195) to 324/(324 + 194). Note if more relative warming occurred in the upper atmosphere, as might be expected since the incoming forcing starts here, during the rebalancing, the end fraction might be different. For example, 324/(324 + 194.5) would cut the temperature rise in half. This is an example where a perturbation from an internal forcing, that may diminish in the rebalancing process, produces a smaller change than that from a constant external forcing.
When testing solar forcing, we kept parameters at the baseline value and increased the solar input of 342 Wm-2 by a factor of 236/235 since after a proportional increase in cloud and surface albedo, this produces a net solar input increase of 1 Wm-2 from 235 to 236. The surface temperature increase was 0.3058 C, close to the expected 0.3064. For a 1-Wm-2 decrease, the surface temperature decrease was 0.3068 C, caused by a slight departure from linearity of the surface temperature sensitivity factor, 1 / (4 s T 3) that decreases with temperature.
A2. Model Results with 1 Wm-2 Longwave Forcing @ the TOA and Evaporation Increase 6% / C
We next will cover using the 2009 data with longwave forcing at the top of the atmosphere combined with a surface evaporation increase of 6% / C. Using the 2009 data which is unbalanced to start, we must first establish an initial equilibrium state using the initial data. This is shown in the table below by comparing the first and second columns. Note after balance, the surface temperature increased from 16.087 to 16.317 C and all the fluxes increased.
_________Present ___Balanced __1 Wm-2 @ TOA __Forcing Change
Surface 396 397.265 398.073 0.808
Ts [C] 16.087 16.317 16.464 0.147
Downward 333 334.128 335.677 1.549
Outgoing 198.5 199.170 200.096 0.924
Window 40 40.128 39.204 -0.924
Evaporation 80 81.108 81.816 0.707
Sensible 17 17.054 17.089 0.035
Notes:
1) Atmosphere absorption = 78 Wm-2 and net solar to surface = 161.3 Wm-2 in all cases.
2) “Present” is from Figure 2 from Trenberth et al and is not balanced since there is a net 0.9 Wm-2 being absorbed by the surface. The “Balanced” column is the solution that adjusts all values so net solar in equals net longwave out. Note that Outgoing + Window goes from 238.5 to 239.3
3) In “Forcing Change” column Surface + Evaporation + Sensible = Downward; Outgoing + Window = 0; Downward and Outgoing changes are in same proportion as “Present” totals.
A3. Definition of Climate Sensitivity and Feedback Terms
We will use the following terms:
F2x = the watts per square meter forcing at the top of the atmosphere (TOA) caused byy doubling of CO2 in the atmosphere = 5.35 ln(2) = 3.71 Wm-2 (3.17 watts per square meter).
k (kappa) = the temperature sensitivity factor or the surface temperature change per Wm-2 of forcing at the TOA. Units are C / W-2
k0 (kappa zero) = surface temperature change per Wm-2 of change of radiation from the surface.
b = a feedback factor for a particular feedback mechanism is the change in forcing in Wm-2 per C of temperature change at the surface. Present practice has the forcing at the TOA, while with our model in is not restricted to only there.
l (lambda) = the surface temperature change before feedback = F2x k.
f = bk = the feedback product, or sometimes feedback value or just the feedback, for a particular feedback mechanism. It is a dimensionless number but we use C / C since it is an additional change in surface temperature per C of any previous change. It does not including additional changes from itself. This is determined after all the feedbacks are combined in the second equation below that is equivalent to a sum of an infinite series of descending terms of this type.
fT = the algebraic sum of all the feedback f values.
Then the final surface temperature change is
F2x k / (1 – fT) = l / (1 – fT) = lmf
Where
mf = the feedback multiplier = 1 / (1 – fT).
Note that k is used to calculate both the pre feedback value and each feedback term.
Present practice uses a single place of forcing and a single value of k so all the b terms can be summed before being multiplied by k. Our new method allows forcing and feedback at different locations so each may have a different value of k and a different value of b compared the present method.
A4. Estimating Surface Evaporation Changes with Temperatures
A4a. Basic Physics Theory and Measurements
Basic physics indicates that surface evaporation rate is proportional to the difference in the water vapor partial pressures of the water and the air at the interface, accelerated by factors such as wind and wave action. Architects and engineers have used such formulas in designing rooms for indoor swimming pools regarding how much air must be changed to maintain relative humidity targets (see ASHRAE handbook). The U.S. Dept. of Energy has expanded this work to include outdoor pools. Experimental data and multiple regression techniques have improved the equations to include wind velocity while also verifying the proportionality with the difference in the water and air partial pressures (water partial pressure equals that of saturated air at the water temperature). In these cases actual evaporation is easily measured by water level drop in the pool. Swimming pools also use an empirical “activity” multiplying factor based on usage.
Some climate models use the mixing ratio and some use specific humidity, but these are related and proportional to partial pressure. So these equations all show that for constant wind speed the evaporation rate is proportional to the differences in the water partial pressure (saturated water vapor pressure at the temperature of the water) and the surface air partial pressure (saturated water vapor pressure at the temperature of the air times it relative humidity expressed as a fraction).
Water saturation vapor pressure is an important physical property that has been studied for many years in fields including climate science. It can be accurately measured in the lab.
Various equations based on the Clausius Clapeyron (C-C) relation can be used for this, but over limited temperature ranges there are same empirical equations that give more accurate results. One of these is Flatau et al (1992) and another we use is from Bolton (1980) that over the range of –35 C to +35 C is within ± 0.3%.
(A1) P = 6.1122 exp(17.67T / (T + 243.5) mb
with T in degrees Celsius.
Using these equations for a given wind speed and wave action, at the mean global the temperature, the evaporation rate increase is about 13% / C for the same rise of water and air temperature if the water vapor content of the air is held constant and about 6% / C if the water vapor content rises to maintain a constant relative humidity (RH), the present assumption in most of the estimates. We have seen no evidence of any climate scientists disputing these basic facts. One problem with the climate models is that they estimate no evaporation for zero wind speed. Data on indoor swimming pools show this is not true and tests on outdoor pools show a evaporation at no wind about one half of that at 2.1 mph. Evaporation proceeds with no wind because the moist air at the surface becomes less dense as its water vapor content increases causing it to rise, and the cooled water at the surface descends. This constantly refreshes the water-air interface. (In seawater this effect is accelerated since the evaporation increases the salt content water causing a greater water density increase). The actual rate change of evaporation for constant RH for water temperatures in the 5 to 25 C range with air temperature either equal, warmer or cooler than the water varies from about 6% to 7%, with smaller percentages at the warmer temperatures.
The problem here is concerned only with the change with surface temperature and here it is better to use the ratio of two values rather than their differences. If global wave and wind activity distributions are held constant, the change in evaporation rate, R, using the equation version with partial pressure,
(A2) R = E2 / E1 = (Pw2 – Pa2) / (Pw1 – Pa1)
Where Pw = the water vapor saturation partial pressure at the water temperature and
Pa = the water vapor saturation partial pressure at the air temperature times r, the relative humidity
If the air and water temperatures are equal and both change an equal amount, and if the relative humidity is held constant it cancels out in the equation,
(A3) R = E2 / E1
= (Pw2 – rPw2) / (Pw1 – rPw1)
= [Pw2 (1 – r)] / [Pw1 (1 – r)] = Pw2 / Pw1
And if the water and air temperatures are within a few degrees of each other and change the same amount with constant RH, the equation is still a good estimate.
Using Bolton’s equation at the mean ocean surface temperatures for both water and air of 17 C rising to 18 C at constant RH gives R of 6.52% / C. A weighted average sweeping from 0 C to 34 C with 1 C rises for each step gives 6.25%. When we let the air be warmer, equal and colder than the water but still rising 1 C we get 6.28%. Wind and wave action will accelerate the evaporation, but we assume these will not change with surface temperature. If they do change, this should be treated as additional feedback.
Data from satellite seems to support these estimates. Wentz et al. (2007) observed that over a period of 1987 to 2006 surface data supported sea surface evaporation and precipitation both increased about 6% / C, indicating there is no obscure reason why actual sea water evaporation does not follow scientific theory.
A4b. The Problem with the Global Climate Models Regarding Evaporation Estimates
While the present simple models do not consider evaporation feedback, the complex GCM models supposedly do. But the estimates from different models of evaporation changes are in the range of only 1 to 3% / C. This writer is not familiar with the GCM computer model details and why they indicate such a low rate of evaporation change nor how they account for any related cooling effect. The climate models for evaporation use either the differences in water vapor mixing ratios or specific humidities which are both proportional to partial pressure and should behave as described here. So even if there were some unknown reason why the evaporation rate changed differently from that expected, it is doubtful the computer models would detect it.
Some of the explanations for this low result (Mitchell, et al. 1987) seem to imply that models because of the heat budget restrict the upper atmosphere outgoing radiation so they cannot accommodate much latent heat of the water vapor condensing at the higher evaporation rates. It is hard to see what mechanism would cause this. This reasoning indicates cause and effect are reversed. This also implies the climate models may ignore the additional upper atmosphere radiation cooling to outer space from increased latent heat release warming cloud tops even with the small evaporation changes they estimate.
Another explanation we have heard is that there is not enough energy in the atmosphere to support a higher level of evaporation. However, the energy for evaporation comes from thermal energy of the water molecules and there is ample water below the surface to maintain the temperature. In a simple physics experiment, an open container of water is placed in chamber that is partially evacuated. The water will begin to boil until it cools enough to freeze. No external heat need be added. It seems the climate models give too much weight to radiation action and less to other physical effects and do a bad job of getting the actual water surface temperature correct. The only way to reduce the evaporation rate below 6% is to have the surface air temperature increase more than that of the water surface, or for the air RH to increase with temperature. It is difficult to see how action high in the atmosphere could cause either of these. It would be helpful if the actual water temperature and air temperatures and air RH used in these estimates were published. And what temperature is used as the divisor in the calculation, the air or the water?
We suspect that these models that simulate a contently increasing radiation forcing followed by a constant forcing period do not let the surface water temperature reach its final value, particularly for the ocean. Many of the models assume a limited sea surface temperature rise (since random mixing with lower water levels make it difficult to simulate) so the air temperature increase in the models could exceed that of the water, reducing evaporation estimates. If the water temperature rise is only 25% less than the air, evaporation rate change will be cut about in half. But except near land, air warmer than the water should be rare since the water absorbs both longwave and shortwave radiation, not the air, which is heated by convection from the water surface. So called “surface” temperature is usually defined at the air temperature a few feet above the surface because that is where most measurements have been and are made. But the real surface, land or water is where the actual radiation is absorbed and sent out.
Some of the climate models assume a fixed sea surface temperature rise such as 2 C. It seems that these computer models were not designed to make accurate estimates of the final steady state the actual interface where small changes can make a big difference in evaporation rates. There is a chance that the models do not reach a final state in the water temperature. Climate sensitivity as presently defined is based on the final equilibrium state and there is no distinction made between the actual surface temperature or ocean and the “surface temperature” which is measured in the air close to the surface. For example the surface radiation of 390 Wm-2 shown in Figure 1 is calculated from the estimated global temperature at 15 C. And changes in the radiation are used to estimate a new temperature. The assumption that seems to be correct is that the real global mean temperatures of the actual surface and the air just above it will finally change the same amount, even though mean land and ocean temperatures may be different than each other.
There are some climate models that do estimate actual sea surface temperature with various mixing level depths assumptions. These also show low evaporation rate increases of 2.5% / C. However they also show water vapor content at about 8% / C which indicates increasing RH with temperature. However actual historical data of different latitudes indicates RH drops about 0.5 to 1 percentage point per C. It is well known that estimating cloud formation is difficult as is estimating when clouds will produce precipitation. We feel that either one or both of these is incorrectly underestimated, causing the corresponding relative humidity to increase, falsely reducing the estimated evaporation rate. A test for this would be to run the climate models with a decreasing forcing of the same amount and see if the water vapor content drops 8% / C. If it does not, as we suspect, it indicates estimation of precipitation, that reduces vapor content, is not being modeled correctly.
Based on the above, this writer feels that classical physics supported by measured actual data indicating evaporation rate changes in the range of 6% should be used for the final equilibrium state. Just because the computer models are complex, does not mean their results should trump those based on solid physics and supported by observed data. For the climate response, separate estimates must be done for different response times for land and ocean locations. The land areas will warm faster than the oceans, but global air mixing will moderate the differences. The difficult question seems to be response time of the ocean surface temperatures. In the mean time there will be negative (cooling) feedback in the “pipeline”, not positive feedback, as some now believe.
A5. Model Shortcoming of Handling Cloud Coverage Changes and Improved Method
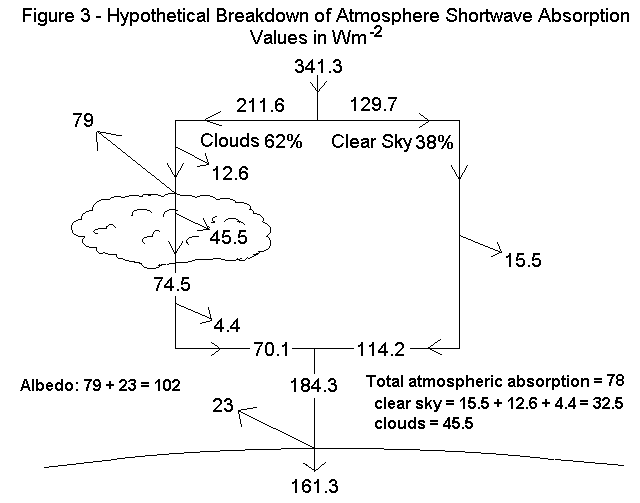
Anyone who has sunbathed knows clouds absorb and reflect more of the sun’s heat than a clear sky absorbs. However, in looking at Figures 1 and 2 a person gets the picture that the only role of clouds is to reflect solar shortwave radiation which is about the same amount as the clear sky absorbs. So what would a person using the model do to estimate the forcing from changing the average cloud coverage? If the cloud cover decreased, for example, the absorption of the clear sky would increase, but the atmospheric absorption from clouds would decrease, and the net solar radiation arriving at the surface would increase as would the surface temperature. At the same, the heat trapping contribution of the clouds would decrease allowing a larger flux to flow out through the atmospheric window, tending to offset surface temperature rise. In order to be able to determine the combined effect of changing cloud cover we estimated by assumption separate factors for cloud and clear sky absorption. Using the data from Figure 2, which has updated data for atmosphere absorption and we understand maintains the cloud cover of 62% from the 1997 data, we made the following additional calculations and some assumptions for illustrative purposes as shown in Figure 3 below:
Fraction of radiation striking the clouds that is reflected: 39.71%;
Cloud absorption of what is not reflected: 37.9% with the remaining transmitted through the clouds;
clear sky absorption for full atmosphere transversal: 11.94%;
clear sky absorption of flux from the top of the atmosphere to cloud top side and leaving bottom of clouds to surface: 1/2 of 11.94%;
flux fraction striking the surface reflected to space: 12.47%.
These numbers are from fine tuning by trial and error to match the data of Figure 2, with the results shown in Figure 3. For 62% cloud cover, clear sky absorption of 15.5, 12.6 and 4.4 adding to 32.5 Wm-2 and cloud absorption is 45.5 Wm-2 for a total of 78 Wm-2 agreeing with Figure 2.
In order to determine the net temperature sensitivity to a change in cloud coverage, that should be linear for small changes, we picked a change from 62% to 60% as a benchmark and determined the new values for the total atmosphere absorption, albedos, and net value of solar radiation striking the surface. From this we used the model to determine the surface temperature change after rebalance, first keeping cloud cover at 62% for longwave greenhouse absorption and then again with cloud cover at 60%. The flux changes were:
Cloud albedo: from 79 to 76.46 Wm-2
Total atmosphere absorption: from 78 to 76.83 Wm-2
Surface albedo: from 23 to 23.48 Wm-2
Net to surface: from 161.3 to 164.53 Wm-2
Using the above changes in the model, but keeping the cloud cover at 62%, produced a surface temperature rise of. 0.869 C. Changing the cloud cover also to 60% in the model reduced the temperature rise to 0.413 C because of reduced cloud heat trapping. These values are for an evaporation change rate of 1.39%. For change rate of 6%, the rise of 0.413 C drops to 0.282 C. Since the above were for a 2% change in cloud cover, divide these by 2 for each 1% change.
A6. Estimating Methods Effects of Ocean Delay
We now consider some methods to estimate transient situation of a faster temperature rise over land because of the higher thermal inertia of the oceans. Most of the evaporation over land originates from rainfall that is partially re-evaporated from the surface or from trees and plants giving off moisture. But most of this rainfall originates from evaporation from the oceans. Assume for example that ½ of the rainfall is re-evaporated with the other half entering the deep soil and/or flowing back to the ocean. Then 1 inch of precipitation originating from the ocean will cause a total of 1 + ½ + ¼ . . . inches that sums to (1 / (1 – ½ ) or 2 inches. Now the question is: “If the oceans do not warm and the land surface temperature rises 1 C, how much will the land evaporation increase?” It will only increase if the fraction that is recycled increases. If that goes up 6% as an estimate, the 0.5 recycle factor becomes 0.53. The total precipitation becomes 1 / (1 – 0.53) or 2.1277, increasing by a factor of 1.064 or 6.4%, slightly more than the 6% of base evaporation. To be conservative and be consistent with the general rate estimated above, we will reduce the estimate to 6.28% / C. The next question is how much of the total global precipitation is over land vs. the ocean? From Trenberth et. al, (2009), land is estimated at 2.06 mm/day and oceans at 3.06 mm/day. Using land/ocean global areas splits at 29.1% and 70.9% this results in a global precipitation of 2.767 mm/day. This agrees closely with the 80 Wm-2 of evaporation latent heat in Figure 3.
Using these numbers, the total precipitation of land is 21.7% of the global total, with 78.3% over the oceans. Trenberth et. al, (p6, 2009) also estimates land and ocean evaporation at 41 and 89 Wm-2 respectively. Using the land/ocean area splits as above results in a total of 75 Wm-2. We raise these 6.7% to get 43.5 and 90 Wm-2 so as to agree with the combined total of 80 Wm-2 in Figure 2. This implies that the land/ocean split of the total global evaporation flux is 15.8% and 84.2%. So land gets a smaller share of the evaporation compared to its precipitation, consistent with the runoff to the ocean.
It can be seen that if the sea surface temperature (SST) rise is less than that over than land, the combined evaporation change rate will be reduced. Using the above percentages, the equation for the combined evaporation change rate, percent per C, of the land temperature rise is,
(A4) R = 0.158 x 1.0628 + 0.842 x 1.0628 DSST
Where DSST is the sea surface temperature rise per C of land temperature rise.
Table 5 shows the results for various values of SST rise for each 1 C of land surface rise. The rates of the GCM climate models in the range of 2% to 3.5% / C corresponds to sea surface temperature rises of about 20% to 50% of the land surface temperature increase. From this it can be seen that the value of 1.39% for many of the estimates used here relates to SST rises of less than one tenth of land rises.
Table 5 – Global Evaporation Rate Increase for Various Sea Surface Temperature Increases for each 1 C Rise of Land Surface Temperature
| Sea Surface Temperature Rise – C | 0.1 | 0.3 | 0.5 | 0.8 | 0.9 | 1.0 |
| Evaporation Rate Increase – % / C | 1.51 | 2.54 | 3.60 | 5.20 | 5.74 | 6.28 |
It should be pointed out that the values in Table 5 assume that the air and surface temperatures for the sea both increase by the same amount and the same applies to the land. Much of the climate models were done with a fixed predetermined sea surface temperature rise at equilibrium of 2 C, but the models have the air temperature at the surface increasing somewhat more than 2 C. This partially explains the low increase in evaporation. In the real climate the surface – both land and sea – absorbs most of the heat from both shortwave and longwave radiation and it then warms the air above. So air temperature at the water surface should not average above that of the water, except in small areas near shore where warmer land temperatures may play a role.
A6a. Land and Ocean Thermal Delay Effects on Respective Surface Temperature Rises
We now consider the case of an exponential increase of annual atmospheric CO2 content. With CO2 forcing estimated as a logarithmic function of ppm concentration, this results in linear increase of Wm-2 forcing with time, also known as a ramp function. While the IPCC models used an annual CO2 ppm increase of 1%, data over the last 10 years show that it is closer to a 0.5% rate, resulting in a doubling in about 140 years. Because the thermal inertia of the ocean is greater than that of land, evaporation cooling that depends mostly on sea surface temperature will be delayed. So rather that heat being stored in the “pipeline” in the ocean to later accelerate global warming, it is negative feedback that is delayed, and it will later reduce the annual rate of warming as the sea surface temperature rises. There are two basic types of heat storage: lumped and distributed. In the lumped type there is only one level of thermal resistance, R, to limit the heat flow in to a single heat storage media with capacity C. We consider the atmosphere in this category since there is so much heat transfer and mixing in it. On the other hand, soil is an example of a distributed heat storage because of the thermal resistance of the soil limits how fast heat can be absorbed by the lower layers. The first layers warm quickly, but lower layers are delayed.
For lumped heat storage with a single time constant of RC, it is easy to calculate the delay of the response for a ramp forcing function. After several time constants, it will be a ramp function parallel to one with zero response time, delayed by one time constant. For all times, the temperature rise vs. time will equal a ramp of zero delay minus an increasing transient starting at zero and a final value of the temperature change in one time constant.
(A5) T(x) = T0 (x) – A(1 – e-x / t )
Where T(x) is the temperature rise at time x, T0(x) is the temperature rise at time x for a zero delay, A is the temperature rise for T0 in one time constant and t is the time constant R x C. Note the time units of x must equal that of t which depends on the units of R and C. We use °C / watt for R and watt-hours / °C for C, so RC and t are in hours.
For the distributed type of heat storage, after a certain delay time the temperature will rise at the rate somewhat less than that of the ramp input. In considering land, we have the lumped atmosphere and the distributed soil. Simulations done by the writer for heat flow and storage in soil depths from 50 to 200 meters in 1 meter sections show that for estimates with soil depths greater than 100 meters, for a forcing of a ramp function, the surface temperature is about 80% of the value corresponding to that of zero delay after 1 year, 95% after 10 years and over 98% after 100 years. This for a 1 x 1 meter column of air and soil with the atmosphere heat capacity at 2834 watt-hrs / C, typical soil heat capacity 702 watt-hrs / C / m^3 and thermal resistance of 0.58 C / watt / m. For a step function of forcing, the surface temperature quickly reached 50% of its final value in only about 0.1 year, 90% at about 0.7 year, then increasing much slower typical of a distributed system, taking about 2 years to reach 95% and after 20 years still below 99% of the final value.
The thermal inertia of the ocean is much more complicated because of mixing between layers which can vary in depths for various ocean locations, and it is beyond the scope of this paper to estimate it. However the ocean thermal delays are considerably longer than those of land. As a typical example we will assume a sea surface temperature delay 10 times the land example above. For this we calculated the delay of the sea surface temperature rise compared to that of land, assuming no heat transfers between land and ocean air masses which gives the largest differences. Keep in mind we are only concerned with the sea surface skin temperature since it affects evaporation rate, not temperatures at greater depths that will have considerably longer delays. For this we used a ramp forcing of 100 years and normalized the final temperature rise to 1 C for a case with instant response to the forcing. Table 6 shows the results. The evaporation rate increases are from the above equation. It can be seen for this case that after 10 years, a short time compared to that for CO2 doubling of over 100 years, the evaporation change rate of 5.2% is significantly greater than 1.39% implied by previous simple climate models. The average value from 10 to 100 years is 5.9% / C, indicating a value of 6% is a reasonable approximate estimate for long term projections.
Table 6 – Sea Divided by Land Surface Temperature Rise vs. Time with Ocean Surface Delay 10X Land Delay and Effect on Evaporation Rate Increase
| Year | 1 | 3 | 10 | 20 | 30 | 100 |
| Sea / Land Temperature Rise | 0.42 | 0.67 | 0.80 | 0.90 | 0.92 | 0.96 |
| Evaporation Rate Increase – % / C | 3.17 | 4.50 | 5.20 | 5.74 | 5.85 | 6.06 |
These evaporation rates can be handled by incorporating the new rate into the energy balance climate model as we did with the results in Tables 1 and 2, of by using the implied 1.39% of the present models and treating the extra cooling as negative feedback. The second method is better because (1) it is a true feedback since the change in cooling depends on the change in surface temperature regardless of the cause, and (2) feedbacks interact with each other; that is they feedback on each other. So adding a negative feedback to a system with a pre-existing positive feedback will have more effect when the positive feedback is large. Feedback fractions must all be combined algebraically, and one feedback multiplier is then calculated.

Dr. Petschauer has presented his second paper for your review and comment. This paper is written for scientific audiences whereas his G6 paper was intended more for public audiences. There is a lot of material here. I look forward to reading your professional, objective reviews.
Richard,
I have a different view of the source of negative feedback due to evaporation. It may in the end just be a different way of saying effectively the same thing as you explained in greater detail, but in a simpler way. You can judge this yourself.
The NET amount of energy that reaches the oceans and ground is only dependent on the solar radiation that passes through the atmosphere, plus a small amount absorbed by the atmosphere from the incoming solar radiation, and that was eventually radiated to the ground. This solar energy in is balanced by removal by three processes: radiation, evaporation (along with convection up), and conduction (along with convection up). The evaporation is the main source of energy removal. The only way evaporation can increase is by a reduction in NET outgoing radiation from the surface, and or by conduction (along with convection up) from the surface. Some of the radiation is direct to space through the "window" in the absorption spectra. The atmospheric greenhouse gases such as water vapor and CO2 block direct transfer of the rest of the outgoing radiation (i.e., it is absorbed and re radiated omnidirectionally). The direct radiation to space is slightly reduced by increases in the greenhouse gases, and the effective absorption path lengths of the atmosphere are changed by the amount of greenhouse gases, so the fraction of energy removed by evaporation becomes larger as greenhouse gas concentration increases.
Measurements have shown the absolute water vapor content near the ground has increased as average temperature increased, as expected. However, the absolute water vapor content at the mid to upper troposphere has held near constant, and recently has even dropped a small amount. This means the water vapor is transported by convection to a limited altitude and condenses out to clouds and precipitation. This likely would result in a reduction in lapse rate in the lower atmosphere due to increased latent heat release with altitude, followed by an upper atmosphere with a dry adiabatic lapse rate, and a slightly raised average location of outgoing radiation due to just the increased CO2.
Since the temperature is a result of the effective location of outgoing radiation to space and the integrated lapse rate from that altitude, there are two competing factors for the amount of net temperature change from CO2 increase. The increase in altitude tends to increase the integration distance for the lapse rate, and the decrease in lapse rate at the lower altitudes due to the latent heat release tends to oppose the net value of temperature increase. Changes in clouds may also affect the net due to change in albedo, but that is for another discussion.
The increase in ground temperature is not caused by back radiation, but back radiation increase is caused by the increase in temperature due to raising the location of net outgoing radiation to space.
I agree with the key point of this post. This blind spot seems to widespread in climate science: Ray Pierrehumbert in the previous post, the recent paper by Lacis and Schmidt, Judith Curry's blog, the Scienceofdoom blog, all concentrate to excess on radiative heat transport.
To criticise the post, it is too long, and I do not have the time to study it in detail. The sections and equations should really be numbered. Without this it is difficult to comment on it in any detail.
To summarise mathematically what I understand as the main point (also made by Leonard), heat is lost from the surface by radiation, convection and evaporation. Let's call these heat fluxes Fr(T), Fc(T), Fe(T). All of these are increasing functions of the surface temperature T (a hotter surface will have stronger convection and faster evaporation). Now in equilibrium,
Fr + Fc + Fe = I,
where I is the incoming radiation (SW+LW).
Now suppose we make a small change to I, dI.
Then the corresponding change in T, dT is determined by
(Fr'(T) + Fc'(T) + Fe'(T)) dT = dI.
Since the three derivatives are all positive,
the value of dT is significantly lower if we include all three effects than if we just include radiation.
Regarding Paul’s comments, he does summarize the basis for the paper in that all three heat transfers from the surface must be considered, not just radiation. What my paper does is provide a way to quantify this based on how much the evaporation rate changes as a function of temperature using a simple approximate method (see section 6e) and a full energy balance solution using Trenberth’s mean global energy balance estimates (initial section 6 parts) where means are also given to convert these to negative feedback values so they can be combined with other feedbacks such as from water vapor.
Note to Ed: Thanks for adding section and equation numbers. And by the way, “Dr. Petschauer” sounds good, but I cannot claim the title. I have a BBA and BEE (1956) with graduate work in advanced calculus. Following retirement from the computer technology field, I have developed statistical software tools for technical work and have been doing independent research on global warming for several years.
Leonard commented on evaporation that:
“The only way evaporation can increase is by a reduction in NET outgoing radiation from the surface, and or by conduction (along with convection up) from the surface.”
It does not seem that radiation balance theory can trump or control the basic physics of evaporation, but must adapt to it. Evaporation rate is discussed in the appendix of my paper. The energy comes from the temperature of the water, not from the atmosphere, and is inhibited by the water vapor content of the air at the interface. The cooled water at the surface drops, and the moist air rises. This refreshes the interface even with no wind speed (contrary to many climate models that show no evaporation at zero wind). If somehow radiation balance can limit the heat leaving the surface, can it also slow down forest fires?
Regarding forcing causing unbalance at the top of the atmosphere, on what basis does present climate theory claim that the surface temperature must increase as much as that at the emission level? It seems that all the clouds and greenhouse gases below it will attenuate the temperature change by the time it reaches the surface. If so, the lapse rate will change because of increased CO2 content and cannot be used to estimate the surface temperature change.
Hello all.
I found this paper most interesting because I have been concerned about the inadequate treatment of evaporation in AGW theory especially as regards the idea that downward longwave radiation can heat up the ocean bulk.
As far as I can see all DLR must get used up in the process of creating extra evaporation with most likely a zero effect on the natural background flow of energy up from the oceans to air despite some warming of the ocean skin.
Are there any ideas on that in the above paper (or elsewhere) which might be helpful ?
I would look at it this way. As greenhouse gases increase, the heat leaving the atmospheric window (that is free of any greenhouse action) reduces a little, so the remaining from the atmosphere must increase to offset the loss in order to restore that leaving to space. But to keep the atmosphere in balance, it must get an equal amount from the surface. The process might proceed as follows: The upper atmosphere warms (since it loses less heat), this eventually propagates down to where the back radiation increases and starts to warm the surface. This will happen sooner over land, but the evaporation will still increase because a larger part of the rainfall will evaporate vs. running off or going into the soil. The added heat from the surface (convection and radiation) warms the atmosphere as does the latent heat from the added water vapor when it condenses into clouds. The model I use assumes the fraction of this added heat received by the atmosphere that goes to outer space to make up the loss from the increased greenhouse action as the same as the total that now leaves (195 out of 195 + 324) or about 37.6% with the rest increasing the back radiation. (I think with increased evaporation, a larger fraction will leave space because cloud formation is at a higher altitude that where most surface radiation is
first absorbed, so our estimates are conservative.)
Over the oceans solar radiation is absorbed in the first few meters of the surface, but longwave IR radiation is all absorbed very close to the surface. The added heat will be broken into two parts. One part will heat the skin surface and the rest will be stored in lower levels depending on the rate of mixing among levels. The effect is to slow down the rate the skin surface heats. The appendix in the paper tries to estimate the role of evaporation as a function of this. But there can be no real global warming unless the ocean surface temperature warms. But as it warms, the evaporation will increase with it pumping latent heat into the atmosphere, reducing the final surface temperature must rise to balance the atmosphere heat flow. In the meantime extra heat coming down till balance is achieved is stored by warming the ocean mixing later. So the ocean merely acts as a slow down mechanism, not the final temperature change.
The solution I use gives balance at all three levels by solving the set of simultaneous equations involved. Note in the above case 100 – 37.6% or about 62.4% of the heat from the surface to the atmosphere increases the back radiation which causes a further increase in surface temperature, etc., similar to positive feedback. This is why all the equations must be solved in a simultaneous fashion. We use well proven matrix linear algebra methods for this.
Richard,
There are two cases for consideration. One is the case where the Earth's temperature is continually increasing, and for this case, the outgoing radiation has to be less than incoming. If the greenhouse gas is increased then settles to a new level, the outgoing radiation may drop for a while and temperature may increase a while, but then the temperature levels off at a higher level, and the radiation out again has to balance incoming.
However, these are not the case I described. If (on the average) the temperature is nearly constant (as it has been the last several years), the outgoing radiation has to be equal to incoming unless there is continual storage in the oceans, and that is not significantly happening. This implies the added CO2 is having a much smaller effect on temperature than AGW predicts. The change in Cp for the continual increase in CO2 is very very small, so the lapse rate is not significantly affected by that. What happens if the CO2 increases so that optical absorption increases for long wave radiation, both from a slight decrease in the "window" direct to space, and by a decrease in effective path length, is that the net energy transfer by radiation from the ground and oceans to space (direct and by absorption and re emission) is decreased, so the energy from the ground and oceans from evaporation and convective heat transfer, carried to a high altitude to be radiated to space, is increased.
The air temperature and humidity level adjust to balance this energy in/out. It is mainly absorption of sunlight that determines ocean (and land) temperature, and the ocean (and land) temperature then drives the air temperature. It is not the air temperature driving the ocean and land temperature (the air only absorbed a small fraction of incoming sunlight). The lapse rate continually adjusts the temperature distribution.
When the average ground temperature is nearly constant, the effective ground and water surface temperature is only (on the average) determined by incoming solar radiation, the effective average altitude of outgoing radiation, and the average lapse rate (=-g/Cp). All the rest is part of the internal methods of re balancing.
Richard,
The point I was trying to make on the previous comment was that back radiation does not transfer heat downward (on the average) to heat the ocean. Only sunlight heats the ocean.
Leonard,
I agree with your points.
My paper is trying to show for the case of 2x CO2 after rebalance is complete, the surface temperature will have risen much less than IPCC estimates since evaporation increases with temperature (for constant RH) much faster than surface radiation does (about 6% / C vs. 1.4% / C). So to keep the atmosphere in balance the heat transferred by evaporation from the surface to the atmosphere greatly reduces the needed increase in surface radiation, and hence surface temperature, compared to the case of constant or low change in evaporation.
My other point in the paper is that forcings from solar changes have a greater effect than that from longwave forcings, but the IPCC seems to be using a temperature sensitivity factor for CO2 that is closer to that from solar activity. This not only increases the pre-feedback surface temperature increase, but also the effect of feedbacks since the same temperature sensitivity factor is used to convert a feedback factor to a feedback value. See Sections 4b and 4c and Section 7.
It appears that Richard Petschauer recognizes that there is a major error in the numbers used by the IPCC -there is no way that the "backforcing by "greenhouse gases " can almost equal the solar input. The work of the IPCC has been totally proven to be politics and has no relationship to scientific data.
What Richard Petschauer has shown is but one of the many "Blind spots" in the thinking of "climate scientists". They seem to totally ignore the heat sink of O2 & N2 – When an Alberta clipper can blow down across Canada and the United States to as far south as Florida and drop the temperature by 20 to 30 degrees below normal -the energy starved SKY dragoon" want to absorb more heat. Where is the example of CO2 causing any heating? References to "Hidden flaws in the greenhouse theory" and the Book "Slaying the Sky Dragoon" will show how many "blind spots " there are in the non-thinking of the "climate scientists". When DR. Ed gets around to posting my revised G-3 The greenhouse gas effect does not exist” several other "blind spots' will be evident and I'm sure DR. Ed has more that I may have missed.
Richard,
I refer to Figure 1. How is 324 W/m2 back radiation from GHG accounted for each gas? How come back radiation is comparable (actually bigger than) with incoming solar radiation when you have 107 W/m2 reflected solar radiation? Has anyone confirm those data from Kiehl and Trenberth? If those data were wrong why this figure used as standard for discussion?
With the benefits of doubts, I assume all those data on the Figure 3 are correct. Total incoming shortwave absorption is 78W/m2. How do you compare this 78 W/m2 with the back radiation of 324 W/m2 in Figure 1? Should the back radiation be no more than 78 W/m2? Where is the 324 W/m2 comes from? If the Earth surface absorbed 168 W/m2, how come the Earth surface radiation has a 390 W/m2? Is it a Grade 3 student's mathematical error performed by Kiehl and Trenberth as well as the Climate Science community, who adopted Figure 1 without querying where are those figures coming from?
If the Earth surface absorbed energy at 168 W/m2, the Earth's asphalt road surface could reach as high as 60 deg C, then the atmospheric temperature must reach burning hot to have a 324 W/m2 back radiation but the sky atmospheric temperature is way less than the ground surface temperature. Has the Climate Science community queried Kiehl and Trenberth's data?
Response to Sam Cheung
You have several questions. First of all the values in Figure 1 have been widely used and are accepted as generally accurate. Figure 2 is an update, but the reference for Figure 1 has a better explanation of the methods used. Much is based on satellite data.
The 390 W/m2 from the surface is based on an estimated mean global temperature of 15 C and the well known Stefan-Boltzmann equation, W = seT^4, where s = 5.67e-8, e = the emissivity constant assumed to be 1 for the surface and T is the temperature in Kelvin (273 + Celsius or 288).
WIth 324 downwelling (back radiation), there is a net radiation cooling at the surface of 390 – 324 or 66 w/m^2. The downwelling tracks the surface temperature but is always less just as the lower atmosphere temperature tracks the surface temperature as defined by the lapse rare. The 324 value is an average of clear-sky conditions and various cloudy conditions. In the reference, clear skies is estimated at 278 W/m^2 and is mostly from water vapor in the lower 1-2 km altitude. Greenhouse gases also radiate heat but the equivalent emissitivity is less than 1 and depends on their thickness. But equipment can read this radiation. For the case of low clouds that act as nearly solid objects for infrared, a simple infrared thermometer can be used. I have read cloud temperatures only about 5 F cooler than the surface so the back radiation is nearly the same as the outgoing from the surface. That is why cloudy night temperature drop less than that from clear skies.
See comment #1 in post G4 on this site for more comments.
Also keep in mind these are average global values over a 24-hour period. Direct sunlight is about 1368 W/m^2 as it enters the atmosphere. Values of about 1000 Wm^2 at the surface are used for solar heating and solar cells estimates. These and other things in direct sunlight get hot at 1000 W/m^2, but they don’t melt.
Sam Chung,
I want to add that the term back radiation is confusing. The ground gets energy from sunlight which heats it up some, and then the ground radiated longer wave thermal energy up. The optically absorbing gases and clouds prevent most of this radiated energy from going directly to space, so act as RADIATION INSULATION. However, surface evaporation of water and atmospheric convection of the air upwards can and do transport most of the energy to a high enough altitude to radiate to space. You have the case of radiation insulation but convective heat transport. I am sure you are familiar with how insulation works. It does not heat the surface it covers, but slows down heat transfer, so if a surface is continually fed energy, it gets hotter than otherwise (think a blanket covering a person). While the mixed energy transport make the atmospheric greenhouse gas effect more confusing than a blanket case, if you read my and Al's description of what is happening you would better understand it. Back radiation is not the cause of heating, it is a result of the combination of effects. However, many people get cause and effect confused, and you can come to the same final result if you go through an analysis that assumes the back radiation is doing the heating. However, for those cases you are actually doing nothing but working backwards from the known answer to match up terms.
Comment on Back Radiation
So called “Back Radiation” is real and “Laws” of thermodynamics properly understood in the light of electromagnetic radiation do not disprove its existence. For one thing it can be measured with present low cost (less than $100) infrared thermometers and from this estimate actual heat being radiated from most solid objects. But not accurately from greenhouse gases that emit over limited wavelengths. The meter makes the gases look colder than actual and thus heat flow out is underestimated. More expensive equipment is needed for this. Yes, energy in the form of infrared energy can be moved from a colder object to a warmer one, but not more than received. So the net heat flow is not from cold to hot objects. But that does not mean the flow is zero.
Some examples: a TV remote passes IR signals to a TV set that may be warmer than the remote. An AM radio receiver picks up stations that are very far away because the wave bounces off the cold atmosphere. Do photons before leaving greenhouse gases or clouds in the atmosphere first check with the earth’s surface to see if it is warmer or colder?
But this “Back Radiation” it is not the “cause” of greenhouse warming but results from it and interacts with it. But it can be a useful tool in estimating how surface temperatures vary with changes in greenhouse action and related feedback responses. An important concept ignored by many climate scientists, including many on this website, is that besides heat balance being required between the planet and outer space, it is also required for the atmosphere as a separate entity and also the surface. The radiation down to the surface and back are parts of the equation, and it is real heat transfer. In fact this is a type of feedback. If one injects more heat to the earth’s from the sun for example, the warmer surface warms the air above and the water vapor in the lower atmosphere gets warmer and sends more heat back to the surface, which warms the atmosphere more, etc. It does not require the top of the atmosphere to warm. That will happen later as convection moves some of the heat upward and may cause additional changes. And if more latent heat is moved from the surface to the atmosphere, less radiation and hence a reduced surface temperature results for the same heat into the atmosphere to balance the heat leaving it at the top. Hence large negative feedback that is now being ignored.
The error in those that think the only concern is balance at the top of the atmosphere is the idea that the lapse rate is somehow fixed independent of the heat added to the atmosphere. So if the temperature at the emission levels increases a certain amount because the atmospheric window shrinks from more CO2, the surface will increase the same amount of degrees. Lindzen questions this assumption. The lapse rate is considerably less than that caused by the pressure drop with altitude because heat is being added throughout. Convection only moves the heat upward, not downward; it does not add heat. What are the sources of the added heat? The absorption of the greenhouse gases, mostly water vapor in the lower 1-2 km, any clouds below this level absorbing longwave from the surface, shortwave radiation in clear skies, solar radiation entering cloud tops, it is not all reflected – cloud cover is about 60%, but cloud albedo is only about 23% and it is not all passed through, and finally the latent heat from water vapor condensing into clouds that depends on global evaporation rates. How can the lapse rate stay fixed when surface evaporation increases 2 to 4 times faster with temperature than does surface radiation? That was the basis of this paper that I never got any serious questions about except the conventional idea that a fixed lapse means we can ignore this and only be concerned with TOA energy balance. This confirms my premise. Even the skeptics here have a “blind spot” to evaporation cooling.
Richard Petschauer,
I haven't found time to read the article (I did try, but will have to focus more), but I have read over some of your comments. If I understand the comments and they accurately reflect your model, then it seems to me you are simply assuming that equilibrium in energy exchange is achieved in negligible time. Are you stating that energy into the earth = energy out from the earth?
I see no appeal to any accepted physical laws or analysis as to why that should be true. [If you aren't assuming that, please keep reading this comment so you can reply, if you wish, relative to the analogy I use and the comments that follow it.]
To use an analogy: We have a bath tub. The water entering from the faucet above is the sun energy. The water leaving from the drain is the earth energy released back into space. Adding CO2 can be modeled as recapturing a few of those drops that leave and putting them back in at the top. For at least a certain amount of time, the bathtub water is not in equilibrium. At some point the drops re-diverted to the top of the tub will raise the water level (and pressure at the bottom) so that more drops will then start to leave than come in from the main faucet and so that the difference eventually (at equilibrium) equals the drops diverted back into the tub. The approach towards this equilibrium position can be fast or slow. It can approach via a decay exponential, overshoot and oscillate (eg, at some point more water is leaving than coming in), or approach through some other behavior. Instead of analyzing the earth from basic principles (and I admit that's asking for a lot within a few comments), you seem to simply assume that equilibrium is instantaneous thereby [* see below] avoiding any raise in water level (ie, any increase in earth surface temperature). If you aren't assuming net zero gain/loss of energy (meaning that equilibrium isn't achieved instantaneously), please clarify in a reply, and I hope to read the details in the article when I can focus sufficiently to read it through. But if greater greenhouse gases were not leading to greater temp, from nonzero time constants where energy is essentially accumulating, the whole model of green house gases being a reason for the earth to warm beyond the no atmosphere case would be ignored. Ignoring that is not justified by many decades of physics analysis and modelling, and you would have to provide the corresponding basic principles in your new theory so that others could test it.
I know you gave little information in your comments, but your idea that extra energy from one place must be balanced elsewhere far away smells to me like you are doing the above — simply solving equations at the moment when equilibrium is assumed to be established. And if your model only includes this information, then I think you are assuming instantaneous equilibrium with whatever set of values you solved.
Now, to address the "[* see below]": More correctly, if you assume equilibrium and then use energy values that don't add up to zero net (eg, if the number you use up and down were to not add up to zero for the whole atmosphere), then you would actually be solving for a permanent state of imbalance.
It really isn't clear to me what you are saying, but this explanation/conclusion above is the best I could do for the moment.
***
I did skim a bit of the top of the article (and elsewhere) and have a concern.
In trying to follow up on some of the references, I noticed (Monckton 2008) has been criticized a fair amount, eg (via google), http://www.altenergyaction.org/Monckton.html . One of the many points mentioned there (if maybe minor) perhaps applies to this paper as well, that IPCC 2007 "DT" value is not 3.26 C but 3.0 C.
Do you have a response to the criticisms of that critique (as apply to whatever part of the Monckton paper apply here)? Were you fundamentally relying on some conclusion or result from that paper that is questioned in that review?
If you use questionable sources, it lowers the likelihood people will take the time to discern what you are presenting.
I didn't check other references or read much, btw, as that reference was right up near the top when I started to read the paper and ran into that potential wall.
I will try to go through the article again but did want to leave this comment now in case I postpone the study again.
BTW, from the little I have read, you present at a high level some criticisms about current mainstream climatologists that, if true, would suggest at least that there might be room to improve the current models to address such criticism, but I fear that perhaps those effects are negligible or accounted for to first order, even if indirectly; that you don't understand the models as well as you state; or even that a solution would not be based upon the math you present. [This is just a hunch I have. I'll try to give the article a fair shake if I can get myself to follow the details. I am not a scientist by profession so I am reaching back to my days of studying physics. It is always a good thing to be able to improve current models.]
Starting afresh on the article. The main argument in the article seems to be that water vapor will greatly reduce the effect of greenhouse gas. (right?)
I'm realizing I may have jumped the gun with my first comment (which reflected my confusion with your comments). If you solve with differential equations varying over time then you may not have a problem.
I'll keep notes to myself as I read, asking as little as possible until I've read a lot (yet still have unanswered questions and hopefully useful comments).
OK, here is one safe remark: It seems there is an incomplete sentence (no verb), and I couldn't figure out what was intended.
>> But as can be seen from Figure 1 with the 78 Wm-2, the perturbation from a change in evaporation caused by a surface temperature change between the surface and the atmosphere, not at the TOA.
I am not sure if I will spend the time to try and reverse engineer the linear equations involved but not presented (I may try to later out of curiosity). However:
The analysis above (mostly simple ledger "accounting" of time-independent power values from a measured set at some point in time), from everything I have read and think have understood, is probably very wrong. Solutions above appear to use no differential equations (in contrast to the much more realistic IPCC models which do repeatedly across sub-components — using comparable small step difference equations, I assume).
I also strongly suspect (despite my limited knowledge of the IPCC models) that the descriptions above (methods 1 and 2) do not describe anything but simple parts of some over-simplified models or describe just the boundary conditions of much more complex models used by the IPCC.
As an example of what this simple power accounting doesn't do (with lots of assumptions made on fraction redistribution among the numbers in the ledger): if heating the earth with the greenhouse gases leads to an accumulation of energy/temperature in the lower atmosphere, there is nothing in the analysis above that would appear to deduce such a value and future effects. For example, and as an extreme hypothetical, if the net flux out into space goes down by 10% for a few years, during which time the surface temperature rises a great deal (as dictated by the SB law with most of the yearly 10% energy not dissipated instead bouncing around in the lower atmosphere) so that, let's imagine, the surface radiation goes from 390 to 490 as the backscatter power goes from 324 to 400 and some other adjustments take place, it would be true that the analysis presented in this article would have made no attempt to verify such behavior as correct or otherwise rule it out. It assumes the fig 1 or fig 2 values as true for all time (a contradiction itself, since having those 2 sets wasn't just to get more accurate measurements but because the values themselves changed over the years — there is a time dependency).
I don't think there is a short-cut to resolving many differential equations sub-problems (or else a very very complex one) all coupled to the "nearby" sub-problems through boundary values. This is why we use computers. In contrast, a single small set of time-independent linear equations presumably used in this article can be solved (eg, via straight forward Gaussian elimination) on paper in a short time.
I am open to the idea that the analysis here can be proven to be useful to what we might expect if we wait out for some amount of time (say hundreds of years) for the transient effects to die down to a negligible amount, but it surely can't say much useful about the next decade or century since it has no dependency at all on time.
Out of curiosity, did the author consider that more water vapor, rather than lead to certain ledger fractional changes as I think were assumed, instead might allow a much larger amount of back-radiation to remain in the lower atmosphere? How was this possibility ruled out? And with more back-radiation, there is more total flux to redistribute for certain parts of the ledger, leaving room for everything to keep going up even if extra energy (as a "feedback") takes place as latent heat removed via water vapor from the very lower levels.
[As a minor point, the direct solar power absorbed into the atmosphere is not all longwave. As this picture suggests, in particular the top strip showing the sun power curve, with red getting through and white getting absorbed, http://en.wikipedia.org/wiki/File:Atmospheric_Tra… , the ozone consumes a fair amount of uv energy. Greenhouse gases likely consume less but, even if more, surely don't consume all or nearly all of that absorbed into the atmosphere. So the longwave amount used in the analysis would not be equal to the entire 67 (78) value.]
This is just my opinion, that's all. [I'm not a scientist or mathematician although I have some background obviously.] If this article is concluding something correct, I would really like to understand it. The author obviously understands a great deal but maybe is oversimplifying this problem and giving too little credit to existing complex mainstream climate models.
Josex,
You ask many questions, many not related to my paper. First of all, there is a simpler version of my paper at post G10. I recommend you look at that, which may help.
The following comments may also answer some of your points.
Accepted definition of climate sensitivity is the change in surface temperature for CO2 doubling after equilibrium is reached including feedback (reaction) effects fom the initial surface temperature change, and there are no other forcing events. In the real world there are constant changes and equilibrium is never reached, so we have a choatic system that never stabilizes. However, for the purposes of the effects of changes in greenhouse gases one would like to know what changes they alone will produce, so it seems like the climate sensitivity concept is very useful. A separate, but important issue is how long it will take for the full effect (temperature rise) to occur.
There are now two ways to estimate the climate senisitivity. One is the simple type model that treats the average of the planet, as I am involved with, and there are the very complex global circulation models that cannot be verified and in fact have had trouble agreeing with some observations.
You are correct that most of the heat that leaves the surface does not go directly to outer space, but first warms the lower atmosphere. Then due to the temperature drop with altitude, the heat rises from convection and radiation to higher levels in the atmosphere. Finally, the atmosphere becomes thin enough that the radiation to space occurs. For water vapor this is at lower levels than CO2. See my post on the effects of the tropopause.
The main jist of my paper is that the present energy balance models only consider the added heat from the surface deposited in the atmosphere from infrared radiation and ignores the latent heat moving to the atmosphere when clouds condense from the surface evaporation that preceeded it. And for each 1 C rise in surface temperature this heat increases nearly as much, about 4.8 Wm-2 compaed to 5.42 from radiation, assumming the expected 6%/C increase in evaporation for constant RH.
The other paper of mine that I refered to in the preceeding comment is on this site. The full title is:
Does the Tropopause Limit Carbon Dioxide Heat Trapping?
Hey Richard, my concerns currently are the following (and I think they have to do with this paper):
— As interesting as the points are and as true as it could possibly be that current models might not do water vapor sufficient justice, I don't think the approach you took to solve for various variables by ignoring the time dependency is the way to resolve the net effect of that excess water vapor. From the bit of research I have done, it's understood you can't get an exact value for the equilibrium climate sensitivity value (2xCO2), but there are methods used to estimate it that involve integrating over the precise path the temperature takes over a period of years (subject to the assumptions required of course). Any attempt to resolve this sensitivity value has to consider that over time the power balances will not at all look like either figure 1 or figure 2. You method is based totally on the values of fig 1, 2.
— [You stated you don't really know how the complex models work or what the IPCC relies upon. If I only went by your words, I think I would have reason, staying on the topic that is this paper, to question this failure to both call out these models yet not understand them nearly that well. With this justification out of the way…] I understand it is a major task to figure out what the complex models are doing, but, in the end, it is difficult to justify a criticism of them without understanding enough of their details (just as my criticism here falls short). One reason why you want to understand the models is that the "missing" water vapor might be taken into account elsewhere, even if imperfectly. Even the creators of those models likely have doubts over aspects of the model and over what is the correct best science, but they likely use a team of experts (computer programmers and various physicists) to help place themselves in the best position. At least some of the complex models were derived from existing understood and proven methods and computer source code for modelling weather. They have leveraged something that works to a large degree. Note: you can find source code for at least one of the models from GISS' website. I downloaded it, and it is mostly a bunch of Fortran code and compiles for *nix operating systems. http://www.giss.nasa.gov/tools/modelE/ http://www.giss.nasa.gov/tools/modelE/modelE.html and I think http://simplex.giss.nasa.gov/snapshots/modelE.201… (or you can look for other related pages.. maybe this as well http://data.giss.nasa.gov/gistemp/sources/GISTEMP… ).
— I am not too interested in less detail (but I will look at G10); I am interested in more! Although I think you hint strongly at the components that are a part of the system of equations you used to make various calculations, why are the exact details not covered (or maybe I missed it)? I would like to see those exact equations, if only to verify your numbers (although what I really want is to understand the details in order to analyze better).
— An oddity that made me doubt it would be worthwhile to try and reverse engineer the equations: the values you get for DT (delta temp?) early on, 0.2149 C, 0.2146 C, and 0.2139 C (see "The resulting surface temperature changes for new equilibrium states were as follows"), are very close to the value you mention immediately afterward, .215 C/Wm^2. The problem is that these two sets are unrelated. The three derived are temperatures, while the other value is a k value. This distinction seems clear because you then use at least some of those temp values in one or more tables and in the text as a temp value while the k value is reused right away in the very next sentence of that section as a k to derive a temp value (admittedly, I have not traced everything through because I have doubts of where the numbers came from so am stalling some further analysis). The units are also clearly stated and are different (C vs. C/Wm^2). With this coincidence in values, however, I do wonder to myself if you made a mistake, and if I don't have good data, it makes it difficult to re-derive your equations.
— Your points in the paper might offer a way to improve the existing models, but the precise knowledge needed and computer source code changes needed require more careful study. If I get an independent project going to document and analyze model E (or any other model), I will leave a note here. [Fortran doesn't seem too difficult, but it and the quantity of code presents a hurdle to get over for sure.. and I don't know how much time I will want to dedicate to this.]
— Did you try to run any of the existing models (eg, the open source ones) with your 6%? [not that doing this would definitively give you your answer, but it would offer valuable clues] Not doing this appears to be an important oversight, given the statement this paper is making.
— Backscattering is an interesting animal. It is like (to use an analogy) if a buoyant ball placed under water was pushing away heavier water molecules as it made its way up, but, rather than the higher up water just sliding around the ball, these molecules would bounce mostly straight upwards and then come down on the ball again and again to keep impeding the ball's flight upwards. By having to deal with constantly bouncing water molecules above it, the ball would take longer to reach equilibrium level. This example is made up, but, if water worked that way, perhaps all of this extra back-bouncing would heat the ball up more than if its path were more easily traversed. The ball essentially has to perform the work of pushing the water out of the way, over and over, rather than just once. Similarly, adding more water vapor to the lower atmosphere might mean that total backscattering goes up significantly, perhaps to more than make up for the extra amount of energy being "deposited" higher up in the atmosphere. The power balance numbers would be higher, including implying a higher surface temp. .. So backscattering is a rather natural effect that can result in much higher values over time than presented in fig 1 and 2 but which you don't appear to consider in your methods. With the equations you used in the paper in hand, I would more easily be able to try and find a contradiction between your methods and more accurate physical modelling (or otherwise acquire support for your results).
— I am not disparaging your arguments; however, like anyone who respects the nature of science, I am not going to easily tear at it without sufficient evidence. Science is always "wrong" and in a learning state, yet I have respect for what has cumulatively survived. Of the many wrong turns taken by science, there might be some important ones wrt climatology. I respect you have valid points (or at least concerns), but the burden on you to justify that your approach is sufficient has to be large, especially when it contradicts the approach normally taken to resolve such variables. [I could give a more sure critique (and ask better questions perhaps) if I knew exactly the system of equations used at various points… sorry to keep repeating this point so much but it's a bit of a disclaimer on my part for not being as specific as I should be.]
— Current climate models make no attempt to match year-to-year temp values but instead try to predict and match (or closely approach) averages over longer time spans (closer to 30-year values). Does your reformulation give correct results if applied to the earth's past historical values? Note the BEST project and recent results, so there is much data at hand over which we have decent confidence.
I doubt I would be the only one to criticize as above if you tried to publish this paper in a major journal on this topic (I'm assuming you haven't tried or would have mentioned it in the text). The conclusions and analysis for deriving some of these values don't appear to be mainstream. If I were in your shoes, I would expect to have to bring more ammo to the table to convince a large number of climatologists of those results (and I agree you have put serious effort already and did acknowledge time constants and other uncertainties). You would gain traction if you could definitively identify a code change to make in one of the models and/or show that adjusting current models to 6% evaporation rate would yield your numbers above (you might have to modify source code to achieve this). Good luck, and I'm curious to know if you think the open source code documentation/analysis and "fork" of model E would be a good idea.
Again, I am not a scientist, but I do have background I think to judge some of this. If I had access to the exact system of equations you used, I think I would be more specific in critique.
Briefly, my disagreement is that, to the degree I understand the variable solving approach taken in the paper, you don't solve using standard physics what the values would be for the different temperatures and many other values. You do use physics and, like everyone else, offer a proxy approach to estimating the 2xCO2 sensitivity. However, you assume (best I can guess) that flux values at key boundaries (or through key areas) would stay constant (over the relevant time span during which 2xCO2 takes place and come to steady state) in testing out a particular 1 W model perturbation. I didn't see you trying to justify these particular constant-through-time assumptions; for example, I didn't see any use of accepted force, power, energy equations/principles to suggest such a scenario is likely. And such assumptions (best I can guess), or the equivalent of such assumptions, are very important to the results you get from the system of equations you used.
Here is an acid test. Did you apply your analysis to the 1997 fig 1 values in order to make a meaningful and accurate prediction of the 2009 fig 2 values and other current globally known values (such as "surface" average temp)? Did you attempt to apply the time constant discussion percentage values in this calculation? If this question is not applicable, what time scale would you say is appropriate? Can you hypothesize (or look up?) what fig 1 value equivalents might be for the year 1850 and then apply your methods to predict 1997 values? What predictive capabilities does you approach offer over existing approaches, and can you find historical data to support such an improvement in prediction power? This type of acid test and these sort of questions are going to be on the minds of many skeptics.
Again, I hope I don't come across as harsh. You can make good points that suggest valuable improvements to the status quo even if the ultimate results derived are not acceptable for some reason or other.
[Note when reading: as of this posting, the first of my earlier today comments is still in moderation.]
If I had to boil down to one question, it might be this:
What justification is used for drawing any relationship between the state variable values shown in either fig 1 or fig 2 and the values of those same variables as they would exist in the future at steady state (which is when the calculation for equilibrium climate sensitivity could be deduced directly)?
A follow up: if the connection assumed in this paper for the usage of those state values from fig 1 or fig 2 to perform calculations of the equilibrium climate sensitivity value is not justified, then what should we expect to get from the calculation exercises performed in this paper? [I don't think the paper derives equilibrium climate sensitivity, in other words, and I am tempted to think that no useful surrogate is derived either.]
My main simplified reasoning to suggest fig 1, 2 values are not to be used directly in a time-independent fashion, as I think this paper uses them, is that, as CO2 is added or water vapor increases, we have to derive the backscattering values (or equivalent) because backscattering greatly affects any flux balance equations. Also, without some sort of time analysis (implied by various physics differential equations), I don't think we can derive such backscattering value(s) at steady state (or at any other necessary time where such value might contribute to the final steady state value).
I think this paper presents useful information, but the overall analysis fails in important ways (eg, as just mentioned), so the final conclusions doesn't follow.
A few points. I have submitted a paper which is an improved version of post 10 (which is a simpler version of this one) to a well know reviewed journal. As part of this I cannot submit it to another one until they decide if they will publish it.
In many cases where a system is perturbed with an outside excitation, it is easier and more meaningful to determine the final steady state solution than the transient analysis that defines how the system behaves before it arrives at the steady state. As an electrical engineer this is one type of thing we study. My analysis is concerned with the steady state solution and one does not need to integrate over time to determine this. You are making things too complicated.
With regard to the complex computer models it is not my job to dig into the complex equations and physics to determine where the errors are when they results do not agree with observations or simple basic theory such as simple energy balance. That would be a fool’s errand.
These complex models should not be confused with weather models. These have improved much in the last 10 to 20 years. Reasonably correct predictions have gone from 2 to 3 days to up to about a week, but this is in large part because of the quick feedback and evaluation of the models and many different versions to weed out the ones that do not work well. I am not an expert in these either, but I am very sure that you will not find the atmospheric content of CO2 in these models, since it does not change in the time interval of interest. So none of their experience improves these climate models. And the climate models have no observation experience whatever in climate modeling estimates vs. results. And they are trying to do this over the planet, not just smaller regions, and over a much longer time period. They are probably all making many of the same mistakes and incorrect assumptions.